3.1. Bezwładność ciał

Obserwator związany z ciałem materialnym, odizolowany od innych układów odniesienia, nie może określić czy znajduje się w spoczynku czy porusza się ruchem jednostajnym względem pewnego układu inercjalnego (to stwierdzenie nie jest zupełnie prawdziwe; patrz 1.1.). Może natomiast łatwo stwierdzić, że porusza się ruchem przyspieszonym lub znajduje się w polu grawitacyjnym (z wyjątkiem przypadku gdyby znajdował się w jednorodnym polu grawitacyjnym).

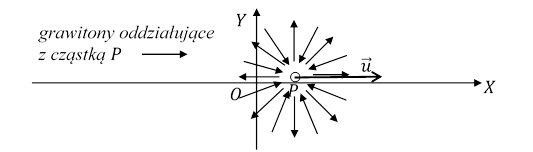
Niech elementarna cząstka materii P porusza się ruchem jednostajnym, w układzie inercjalnym OXYZ, z prędkością wzdłuż osi OX zgodnie z jej zwrotem.

Rys. 3.1.1.

Z cząstką P, w czasie Δt, między jednym a drugim skokiem, oddziałują grawitony przekazujące jej pewien pęd i energię. Suma pędów przekazanych cząstce przez te grawitony jest wektorem zerowym i suma energii przekazanych cząstce jest równa zero. Grawitony te nie zmienią pędu i energii cząstki skutkiem czego nie zmieni się jej prędkość.

Jak wygląda oddziaływanie grawitonów z cząstką elementarną, w układzie OXYZ, gdy zmienia się prędkość cząstki? Jeżeli zewnętrzna siła zmienia prędkość cząstki (cząstka porusza się ruchem przyspieszonym) i pęd cząstki zmienia się o , w czasie Δt, to

Niech w czasie Δt oddziałuje z cząstkę P n grawitonów , które przekazują cząstce pędy gdzie k = 1, 2,...,n. Jak wiemy w układzie inercjalnym OXYZ

Zgodnie z Założeniem 6 tylko absorpcja lub emisja grawitonów może zmienić pęd cząstki. Pęd cząstki może się zmienić o tylko wtedy, gdy z cząstką, w czasie Δt, oddziałuje s grawitonów (), przekazujących jej pędy (k = 1, 2,...,s), takich że suma pędów przekazanych przez te grawitony cząstce jest równa zmianie pędu cząstki. Te grawitony zmieniają pęd cząstki, ale nie działają na nią żadną siłą.

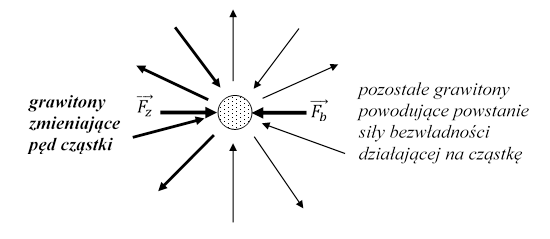
Pozostałe grawitony gdzie k = s + 1, s + 2,...,n starają się zmienić pęd cząstki o

Rys. 3.1.2.

Jeżeli w układzie inercjalnym czynnik zewnętrzny (siła ) zmieni pęd cząstki o w czasie Δt, to oddziaływanie cząstki z przestrzenią i materią, za pośrednictwem grawitonów, stara się przeciwstawić zmianie pędu tak, aby przywrócić poprzedni pęd. Jeżeli to jest niemożliwe, to na cząstkę działa siła bezwładności

powstała w wyniku oddziaływanie cząstki z grawitonami.

Siła bezwładności powstaje w gruncie rzeczy stąd, że z cząstkę oddziałują tylko grawitony p_k k = s + 1, s + 2,...,n, dla których suma pędów przekazywanych tej cząstce jest wektorem niezerowym, skierowanym przeciwnie do wektora przyspieszenia cząstki. Obrazowo można powiedzieć tak. Z cząstką poruszająca się ruchem przyspieszonym, z tej strony w którą jest zwrócony wektor przyspieszenia, oddziałuje więcej grawitonów niż ze strony przeciwnej. Nie liczą się te grawitony, które są absorbowane lub emitowane przez cząstkę tylko po to, aby możliwa była zmiana pędu. Pęd cząstki nie może zmienić się momentalnie. Cząstka musi zaabsorbować oraz wyemitować odpowiednią ilość grawitonów. Energia kinetyczna cząstki zmienia się o wartość pracy wykonanej przez zewnętrzną siłę.

Na cząstkę poruszającą się ruchem przyspieszonym działa siła hamująca skierowana przeciwnie do siły zewnętrznej i równa jej, co do wartości.

Jeżeli w układzie inercjalnym na cząstkę nie działa siła zewnętrzna, to oddziaływanie z przestrzenią i materią nie pozwala na zmianę jej prędkości.

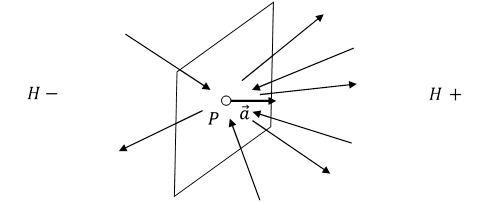
Płaszczyzna przechodząca przez cząstkę P i prostopadła do wektora przyspieszenia tej cząstki dzieli przestrzeń na dwie półprzestrzenie. Przez H + oznaczmy tę półprzestrzeń, w której znajduje się wektor przyspieszenia cząstki zaczepiony w punkcie P, H - oznacza pozostałą półprzestrzeń.

Rys. 3.1.3.

Wniosek I.

Siła bezwładności działająca na cząstkę, poruszającą się ruchem przyspieszonym, jest efektem tego, że z cząstką oddziałuje więcej grawitonów z półprzestrzeni H + niż z półprzestrzeni H -. Tych grawitonów, które nie są potrzebne do zmiany pędu cząstki.

Bezwładność ciała jest wynikiem jego oddziaływania z cząstkami przestrzeni i materii, które znajdują się w kuli oddziaływania grawitacyjnego tego ciała w odległości większej od d_w, za pośrednictwem grawitonów.

Siła bezwładności działająca na ciało jest sumą sił bezwładności działających na cząstki elementarne tworzące to ciało.

W układzie nieinercjalnym (w polu grawitacyjnym) mechanizm powstawania siły bezwładności jest taki sam, jak w układzie inercjalnym. Na ciało, oprócz siły bezwładności, działa dodatkowa siła oddziaływania grawitacyjnego wynikająca z tego, że suma pędów wszystkich grawitonów oddziałujących z ciałem, w czasie Δt, jest wektorem niezerowym ().

Cząstki przestrzeni, tak jak i cząstki materii, mają masą. Z tego powodu działa na nie siła bezwładności, analogicznie jak na cząstki materii. Podobnie jak cząstki materii, cząstki przestrzeni nie mogą poruszać się z prędkością większą od prędkości światła.

Siła bezwładności jest określona wzorem

gdzie m_b oznacza masę bezwładną ciała. Jeżeli możemy uznać, że masa ciała jest stała, to

Średnia zmiana pędu* ciała, przypadająca na jeden grawiton oddziałujący z tym ciałem, jest równa przyspieszeniu, z jakim porusza się to ciało (w układzie jednostek MS*).