1.7. Pęd i energia przekazywane do elementarnej cząstki, za pośrednictwem grawitonów, ze względu na obecność innej elementarnej cząstki
Elementarna cząstka materii znajdująca się w spoczynku, w układzie inercjalnym, daleko od innych cząstek materii absorbuje z każdego kierunku taką samą ilość energii, przekazywaną do niej przez strumień grawitonów. Suma pędów przekazywanych do cząstki przez te grawitony jest wektorem zerowym. Równocześnie, w jednostce czasu, cząstka emituje w każdym kierunku, za pośrednictwem grawitonów, taką samą ilość energii, jaką absorbuje i pędy unoszone przez grawitony równoważą się.
Rys. 1.7.1.
W układzie inercjalnym, energia emitowana z jednostki powierzchni cząstki w jednostce czasu jest taka sama jak ilość energii absorbowanej przez jednostkę powierzchni tej cząstki w jednostce czasu. W wyniku oddziaływania z grawitonami na cząstkę nie działają żadne siły i cząstka pozostaje w spoczynku lub porusza się ruchem jednostajnym i prostoliniowym.
Rys. 1.7.2.
Weźmy element powierzchni ΔS. Oznaczmy przez Kb zbiór wszystkich kątów bryłowych, w kształcie stożka, o wierzchołku 
, mających taką samą miarę Γ, osie do siebie równoległe i tworzące z wektorem normalnym 
do powierzchni ΔS kąt β. Niech Z oznacza zbiór wszystkich wektorów o końcach w punkcie , zawartych w kącie bryłowym należących do zbioru Kb. Mówimy, że grawiton jest absorbowany przez element powierzchni z kąta bryłowego Γ, jeżeli wektor pędu grawitonu absorbowanego przez element powierzchni ΔS jest równy pewnemu wektorowi ze zbioru Z.
Zamiast obliczać pęd przekazywany do cząstki, przez grawitony przez nią absorbowane lub emitowane, wygodniej jest rozpatrywać strumień energii absorbowanej lub emitowanej przez cząstkę. Ten strumień oddziałujący z cząstką, z określonego kąta bryłowego, pozwala następnie określić pęd przekazywany do cząstki przez grawitony. Jeżeli kąt bryłowy ma niewielką miarę i energia przekazana do elementu powierzchni ΔS przez grawitony przez nią absorbowane, z kąta bryłowego, jest równa ΔE, to pęd przekazany przez te grawitony do tego elementu powierzchni jest równy
.
Do elementu powierzchni cząstki o polu ΔS, w czasie Δt, grawitony absorbowane przez cząstkę przekazują energię ΔSEsΔt z kąta bryłowego półpełnego o mierze 2π. Grawitony absorbowane przez ten element powierzchni z kąta bryłowego o mierze Γ przekazują, w czasie Δt, do tego elementu energię
.
Wielkość
ΔS ' - ΔScosβ
jest polem powierzchni rzutu prostokątnego elementu ΔS na płaszczyznę przechodzącą przez punkt O i prostopadłą do osi stożka, określającego kąt bryłowy Γ. Element powierzchni ΔS ' absorbuje taką samą ilość energii, za pośrednictwem grawitonów, jak element ΔS.
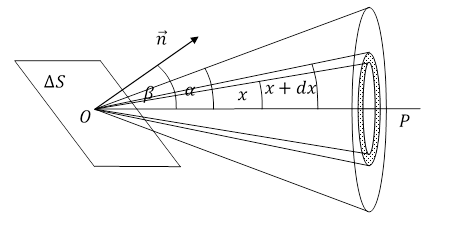
Rys. 1.7.3.
Kąt bryłowy o wierzchołku w punkcie O odpowiadający kątowi x ma miarę
.
Element powierzchni ΔS z kąta bryłowego określonego przez kąt x oraz kąt x + dx absorbuje, w czasie Δt, odpowiednio energię
i
.
Energia absorbowana przez ΔS z kąta bryłowego o mierze 
, z którego wycięto kąt bryłowy o mierze 
jest równa
.
Wypadkowy pęd przekazywany do elementu ΔS z kąta bryłowego 
jest wektorem równoległym do osi OP kąta bryłowego a jego wartość jest równa
.
Całkowity pęd przekazany do elementu powierzchni ΔS, z kąta bryłowego odpowiadającego kątowi α jest równy
.
Weźmy dwie elementarne cząstki P i Q o masach m1 i m2, promieniach d1 i d2, znajdujące się w odległości r < dw od siebie, daleko od innych cząstek.
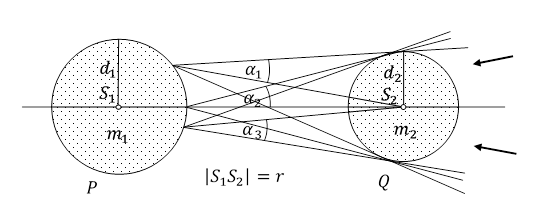
Rys. 1.7.4.
Cząstka Q zatrzymuje część grawitonów, które mogłaby zaabsorbować cząstka P. Podzielmy powierzchnię półkuli cząstki P, zwróconą w stronę środka cząstki Q, na n dostatecznie małych elementów powierzchni ΔSi.
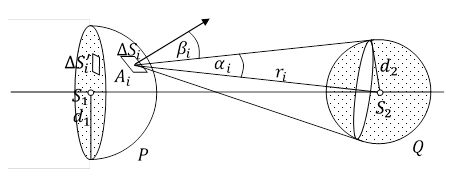
Rys. 1.7.5.
Do każdego elementu ΔSi, ze względu na obecność cząstki Q, nie jest przekazywany pęd
,
gdzie αi jest kątem wyznaczonym przez cząstkę Q o wierzchołku w punkcie 
. Utwórzmy rzuty prostokątne 
elementów ΔSi na koło, o środku S1 i promieniu d1, prostopadłe do prostej S1S1.
ri = |AiS2|
Jeżeli d1 << r, to możemy przyjąć, że ri = r i AiS2 || S1S2.
Pęd, który nie zostanie przekazany do cząstki P, ze względu na obecność cząstki Q, w czasie Δt, ma wartość
i zwrot wektora 
.
Ponieważ
więc
i odpowiednio
.
dla
r < dw .
Pęd przekazany do cząstki P przez grawitony przez nią absorbowane ma wartość p i zwrot wektora 
. Cząstce Q zostanie przekazany pęd równy liczbowo p zwrócony w stronę cząstki P.
Każda cząstka wyemituje odpowiednią ilość energii, za pośrednictwem grawitonów, równomiernie w każdym kierunku. Grawitony wyemitowane przez cząstkę Q nie oddziałują z cząstką P i przekazują do tej cząstki zerowy pęd. Analogiczna sytuacja zachodzi dla cząstki Q.
Ostatecznie na obie cząstki działają siły równe co do wartości ale przeciwnie skierowane (w stronę drugiej cząstki).
Oznaczmy
.
Dla r < dw pęd przekazany do cząstki P ze względu na obecność cząstki Q jest
i siła działająca na cząstkę P jest równa
.
W ten sposób otrzymujemy prawo powszechnej grawitacji w wyniku oddziaływania cząstek materii lub cząstek przestrzeni, za pośrednictwem grawitonów, na poziomie cząstek elementarnych. Otrzymana wartość siły jest wartością średnią. Ze względu na chaotyczne oddziaływanie cząstki z grawitonami, w bardzo krótkich odstępach czasu, rzeczywista wartość siły może się nieco różnić od wartości średniej.
Z porównania tego wzoru z prawem powszechnej grawitacji Newtona wynikają zależności
awhη2 = G
i
.
Wartości h, G, Es, Dw i c są wyznaczone przez obserwatora znajdującego się blisko cząstki P.
Obliczmy ilość grawitonów nieoddziałujących z cząstką P ze względu na obecność cząstki Q.
Cząstce P nie jest przekazywany pęd
.
Średni pęd przekazywany przez jeden grawiton do cząstki P jest równy
,
gdzie Dw jest odpowiednią odległością i wartością stałą.
Średni pęd 
nie zależy od odległości cząstek P i Q. Z cząstką P nie oddziałuje
grawitonów, ze względu na zmniejszenie pędu do niej przekazywanego.
Ze względu na obecność cząstki Q ilość grawitonów oddziałujących z cząstką P jest mniejsza o N1. Równocześnie zmalało ciśnienie wywierane przez grawitony na jej powierzchnię. Cząstka powiększa nieco swoją powierzchnię i dlatego absorbuje o N2 więcej grawitonów (N2 < N1). Te ostatnie nie zmieniają pędu przekazywanego przez wszystkie grawitony do cząstki P, ponieważ oddziałują z cząstką niemal jednakowo z każdego kierunku, ale wpływają na wartość jej masy.
,
i
r < dw.
Tylko przy takim założeniu, co do wartości N2 , wnioski wynikające z przedstawionej teorii grawitacji są zgodne z doświadczeniem i obserwacjami astronomicznymi.
Ilość wszystkich grawitonów nieoddziałujących z cząstką P, ze względu na obecność cząstki Q, jest równa
.
Wprowadźmy oznaczenie
.
Ilość wszystkich grawitonów, które nie oddziałują z cząstką P, ze względu na obecność cząstki Q, jest określona wzorem
dla
r < dw.
Równocześnie o taką samą wartość zmniejszy się ilość grawitonów oddziałujących z cząstkę Q.
Siła działająca na cząstkę P jest równa
.
Przy wyprowadzaniu wzoru dla F przyjęto ri = r. Dlatego ten wzór nie jest zupełnie dokładny. Weźmy dwie elementarne cząstki, o promieniu d = 10-15 m, znajdujące się w odległości r = 1 mm = 10-3 m. Błąd względny, z jakim jest określona siła F, w tym przypadku jest równy
.
Dla większych odległości między cząstkami ten błąd jest jeszcze mniejszy. Ponieważ oddziaływanie grawitacyjne między ciałami jest oddziaływaniem grawitacyjnym między ich cząstkami elementarnymi, więc wzór określający prawo powszechnej grawitacji Newtona, w zwykłych warunkach, można uznać za zupełnie dokładny. Dopiero dla bardzo małych odległości między cząstkami, porównywalnymi z ich rozmiarami, wystąpi odstępstwo od wzoru Newtona.
W wyniku oddziaływania z grawitonami na dwie cząstki przestrzeni działają siły „przyciągania” według tego samego wzoru jak dla dwóch cząstek materii. We Wszechświecie mogą powstać obszary, w których gęstość przestrzeni jest większa od wartości średniej. Również między cząstką materii i cząstką przestrzeni działa siła „przyciągania” określona takim samym wzorem jak dla cząstek materii.
Weźmy cząstkę P, o środku S1 i cząstkę Q o środku S2, znajdujące się w odległości r > dw. Cząstka P emituje grawitony absorbowane przez cząstkę Q. Każdy element ΔSi cząstki P emituje za pośrednictwem grawitonów, w czasie Δt, taką samą ilość energii, jaką absorbuje w tym czasie. Cząstka Q absorbuje energię emitowaną z elementu ΔSi z kąta bryłowego wyznaczonego przez kąt αi (Rys. 1.7.5.). Jeżeli przyjmiemy, że ri = r, to całkowity pęd przekazywany przez cząstkę P do cząstki Q, w czasie Δt, ma wartość
i zwrot wektora .
Cząstce Q jest przekazywany pęd
.
Podobnie cząstka P absorbuje grawitony emitowane przez cząstkę Q.
Cząstce P jest przekazywany pęd
.
Na cząstkę P działa siła
.
W wyniku tego oddziaływania z grawitonami obie cząstki zyskują pewien pęd zwrócony przeciwnie do środka drugiej cząstki. Na każdą cząstkę działa siła odpychania określona tym samym wzorem jak siła „przyciągania” dla dwóch cząstek materii.
Ponieważ dla r > dw z każdego kierunku do cząstek jest przekazywany, za pośrednictwem grawitonów, taki sam pęd, to między cząstkami nie ma „przyciągania” grawitacyjnego.
Ilość grawitonów emitowanych z jednej cząstki i absorbowanych przez drugą, w czasie Δt, jest równa
,
gdzie
jest pędem przekazywanym z jednej cząstki do drugiej przez jeden grawiton.
i jest odwrotnie proporcjonalna do odległości między cząstkami.
Przedstawione powyżej oddziaływanie grawitacyjne między dwiema elementarnymi cząstkami, polegające na wymianie grawitonów między nimi, ma charakter statystyczny (przypadkowy). Wyprowadzone wzory dają właściwe wartości energii, pędu, ilości oddziałujących grawitonów, dla pojedynczych elementarnych cząstek, w długim odstępie czasu Δt. Dla ciał złożonych z bardzo dużej ilości elementarnych cząstek są prawdziwe nawet w bardzo krótkich odstępach czasowych.
Dla elementarnej cząstki materii o masie m i promieniu d mamy
.
.
Podstawiając wartość Dw do wzoru
otrzymujemy
.
Podsumowanie
Weźmy cząstkę P o masie
i cząstkę Q o masie
o środkach odpowiednio S1 i S2, które znajdują się w odległości |S1S2| > dw.
Ilość grawitonów oddziałujących między tymi cząstkami, w czasie Δt, jest równa
.
Ze względu na wzajemne oddziaływanie grawitacyjne cząstce P z cząstki Q jest przekazywany pęd
.
Odpowiednio cząstce Q jest przekazywany pęd
.
Weźmy dwie cząstki materii o masach
Ilość grawitonów, które nie oddziałują, w czasie Δt, z pierwszą cząstką, ze względu na obecność drugiej jest równa
.
Pęd, który zostanie przekazany do pierwszej cząstki ze względu na obecność drugiej, jest równy
.
awhη2 = G
