1.8. Zmiana pędu i energii kinetycznej cząstki materii lub przestrzeni w wyniku oddziaływania z grawitonami

Oddziaływanie grawitacyjne materialnego ciała (złożonego z elementarnych cząstek) oraz pozostałych elementarnych cząstek jest sumą oddziaływań elementarnych cząstek tego ciała z pozostałymi elementarnymi cząstkami, za pośrednictwem grawitonów.

Założenie 5.

Zmieńmy w dowolny sposób pęd cząstki (na przykład działając na nią siłą grawitacyjną lub elektromagnetyczną ) o , w czasie Δt, podczas spoczynku w układzie UW między jednym a drugim skokiem.

Taka zmiana jest możliwa tylko wtedy, jeżeli, w czasie Δt, wśród grawitonów oddziałujących z cząstką znajdą się takie, które przekażą cząstce pęd . Te grawitony zmieniają pęd cząstki, ale nie działają na cząstkę żadną siłą. W tym czasie pozostałe grawitony oddziałujące z cząstką przekazują do niej pęd . Te grawitony nie zmieniają pędu cząstki, ale powodują, że na cząstkę działa siła

.

Każda zmiana pędu cząstki jest możliwa tylko w wyniku oddziaływania cząstki z grawitonami a co za tym idzie z innymi cząstkami. Każda zmiana pędu cząstki powoduje zmiany pędu innych cząstek, tak, że całkowity pęd Wszechświata nie ulega zmianie.

Zmiana pędu ciała jest sumą zmian pędów cząstek elementarnych tworzących to ciało.

Zmiana pędu cząstki jest możliwa tylko w wyniku absorpcji lub emisji grawitonu. Nie ma innej możliwości zmiany pędu cząstki. Stwierdzenie, że pęd cząstki zmienia się pod wpływem działania siły to tylko pewna obserwacja, która nie wyjaśnia, dlaczego ta zmiana jest możliwa. Energia elektronu w atomie zmienia się skokowo, jeżeli elektron wyemituje lub zaabsorbuje foton. Dlatego nie powinno wydawać się dziwne, że pęd i energia cząstki elementarnej zmieniają się skokowo przez emisję lub absorpcję grawitonu.

Wydaje się, że pęd elementarnej cząstki zmienia się płynnie a nie skokowo, ponieważ pęd przekazywany tej cząstce, w czasie Δt między skokami, jest w zwykłych warunkach bardzo mały.

Grawitony oddziaływujące z cząstką można podzielić na dwie grupy.

Pierwszą grupę stanowią grawitony potrzebne do zmiany pędu cząstki. Suma pędów przekazanych cząstce, w czasie Δt, przez grawitony pierwszej grupy jest równa zmianie pędu cząstki w tym czasie. Grawitony pierwszej grupy zmieniają pęd cząstki, ale nie działają na nią żadną siłą.

Drugą grupę stanowią pozostałe grawitony oddziałujące z cząstką. Suma pędów przekazanych cząstce przez drugą grupę, w czasie Δt, określa siłę działającą na cząstkę.

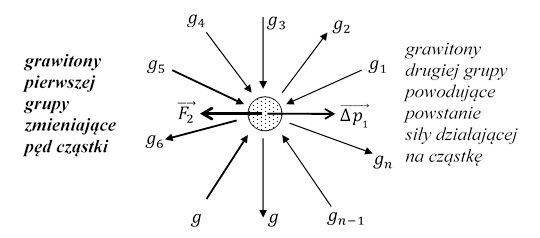
Rys. 1.8.1.

Niech, w czasie Δt, z cząstką oddziałuje n grawitonów g₁, g₂, ..., g_n-1, g_n, które przekazują cząstce pęd

i energię

,

gdzie jest pędem i E_k energią przekazaną cząstce przez grawiton g_k.

Jeżeli k - ty grawiton jest emitowany przez cząstkę, to E _k < 0. Jeżeli k - ty grawiton jest absorbowany przez cząstkę, to E _k > 0.

1) Jeżeli cząstka jest swobodna, to zmiana pędu cząstki, w czasie Δt, jest równa i zmiana jej energii całkowitej jest ΔE. Grawitony pierwszej grupy zmieniają pęd cząstki. Pędy przekazane cząstce przez grawitony drugiej grupy równoważą się i na cząstkę nie działa żadna siła.

Gdy w pewnym przedziale czasowym

i

ΔE = 0

dla każdego Δt, to cząstka porusza się ruchem jednostajnym.

Dla cząstka, w czasie Δt, zmieni swoją energię kinetyczną o ΔE_k i zmieni swoją całkowitą energię o ΔE_c. Między tymi zmianami zachodzi związek

ΔE_k + ΔE = ΔE_c.

Energia kinetyczna cząstki jest częścią całkowitej energii cząstki.

2) Jeżeli zewnętrzna siła zmieni pęd cząstki o wektor , w czasie Δt, to wśród grawitonów oddziałujących z cząstką, w tym czasie, istnieje l grawitonów pierwszej grupy g₁, g₂, ..., g_l, takich że

,

gdzie jest pędem przekazanym cząstce przez grawiton g_k. Pozostałe grawitony drugiej grupy g_l+1, g_l+2, ..., g_n przekazują cząstce pędy . Suma pędów tych grawitonów jest równa

.

Te grawitony powodują, że na cząstkę działa siła

.

Jeżeli pęd

przekazany cząstce przez grawitony jest wektorem zerowym, to

.

Zmiana energii kinetycznej ΔE_k jest równa pracy W wykonanej przez siłę .

ΔE_k = W

Zmiana całkowitej energii cząstki ΔE_c jest równa sumie pracy W wykonanej przez siłę i energii przekazanej przez grawitony ΔE.

ΔE_c = W + ΔE

3) Jeżeli pęd cząstki nie zmieni się w czasie Δt (cząstka jest unieruchomiona lub porusza się wymuszonym ruchem jednostajnym i nie zmienia się jej masa), to pędy grawitonów pierwszej grupy równoważą się, natomiast grawitony drugiej grupy powodują, że na cząstkę działa siła

.

Energia wewnętrzna cząstki zmieni się o ΔE.

Rys. 1.8.2.

Weźmy materialną kulę o masie m spoczywającą na podłodze nieruchomej windy, znajdującej się na powierzchni Ziemi. Spoczynek kuli jest wymuszony ze względu na oddziaływanie kuli z podłogą windy. Na cząstki kuli działają siły oddziaływania grawitacyjnego i siły elektromagnetyczne między cząstkami kuli oraz podłogi windy. Cząstki elementarne tworzące kulę poruszają się skokowo w sposób chaotyczny i ich pędy zmieniają się, w niewielkim stopniu, w krótkich odstępach czasu. Pewna ilość grawitonów oddziałujących z cząstkami jest potrzebna do zmiany ich pędu, pozostałe działają na nie pewną siłą. Jednak suma pędów grawitonów zmieniających pędy cząstek kuli, w jednostce czasu, jest wektorem zerowym.

Kula, jako całość nie zmienia swojego pędu, pozostaje w spoczynku i możemy powiedzieć, że żadne grawitony nie są potrzebne do zmiany pędu kuli.

Od strony środka Ziemi z kulą oddziałuje mniej grawitonów niż ze strony przeciwnej. Wypadkowy pęd przekazywany do cząstek kuli przez grawitony, w czasie Δt, jest niezerowy i skierowany w dół. Oddziaływanie z grawi­tonami nie zmienia pędu kuli, lecz przejawia się w postaci ciężaru kuli naciskającej z siłą

na podłogę windy. Siła nacisku jest wynikiem oddziaływania cząstek kuli z cząstkami podłogi.

Niezależnie od tego czy kula pozostaje w spoczynku czy porusza się w dowolny sposób, ilości grawitonów dochodzących do niej z każdego kierunku są jednakowe (cząstki kuli poruszają się w sposób skokowy pozostając w spoczynku, w układzie UW, między jednym a drugim skokiem). Również pędy przekazywane przez nie do kuli są takie same. Jednak w zależności od ruchu kuli grawitony mogą być w różny sposób wykorzystywane. Część z nich jest potrzebna do zmiany pędu kuli, pozostałe działają na nią pewną siłą.

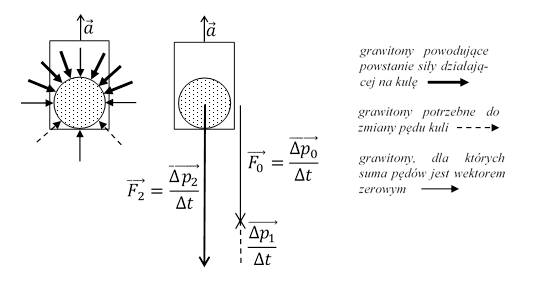
Rys. 1.8.3.

Jeżeli winda porusza się ruchem przyspieszonym w górę, to zmusza również kulę do ruchu przyspieszonego w górę z tym samym przyspieszeniem . Część grawitonów oddziałujących z kulą jest potrzebna do zmiany pędu cząstek kuli. Suma pędów tych grawitonów, zmieniających pęd kuli w czasie Δt, jest wektorem niezerowym

zwróconym w górę. Wypadkowa pędów pozostałych grawitonów, oddziałujących z kulą w czasie Δt, jest wektorem zwróconym w dół i

.

Stąd Δp₂ > Δp₀. Te grawitony nie zmieniają pędu kuli, ale ich oddziaływanie z kulą przejawia się w postaci zwiększonego ciężaru kuli naciskającej z siłą

większą od na podłogę windy.

F₂ = F₀ + ma
 

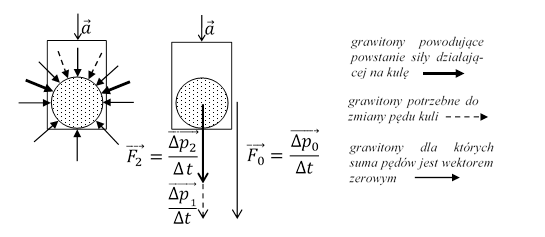
Rys. 1.8.4.

Jeżeli winda porusza się ruchem przyspieszonym w dół z przyspieszeniem a < g, to również kula porusza się z takim samym przyspieszeniem. Część grawitonów oddziałujących z kulą jest potrzebna do zmiany pędu kuli. Suma pędów tych grawitonów, zmieniających pęd kuli w czasie Δt, jest wektorem

zwróconym w dół. Wypadkowa pędów pozostałych grawitonów, oddziałujących z kulą w czasie Δt, jest wektorem zwróconym w dół i

.

Stąd Δp₂ < Δp₀. Te grawitony nie zmieniają pędu kuli, ale ich oddziaływanie z kulą przejawia się w postaci zmniejszonego ciężaru kuli naciskającej z siłą

mniejszą od na podłogę windy.

F₂ = F₀ - ma