3.4. Ruch ciała w polu grawitacyjnym

Weźmy dwóch dowolnych obserwatorów O i O₁ znajdujących się w polu grawitacyjnym wytworzonym przez kulę o środku S i masie M, oraz obserwatora O' znajdującego się daleko od kuli i innych ciał materialnych. Niech dla O, O₁ i O' odstępy czasu między dwoma, tymi samymi, zdarzeniami są odpowiednio Δt, Δt₁ i Δt'.

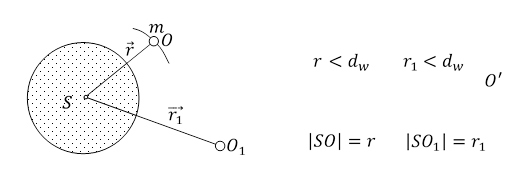
Rys. 3.4.1.

Dla O₁ i O' zachodzi związek

Δt₁ = α₁Δt',

natomiast dla O i O' mamy

Δt = αΔt',

gdzie

Jeżeli dla obserwatora O między dwoma zdarzeniami upłynie Δt jednostek czasu, to według O₁ upłynęło Δt₁ jednostek czasu. Jeżeli O określi masę ciała znajdującego się blisko niego, jako m, to według obserwatora O₁ masa tego ciała jest równa .

Aby określić zależności między wielkościami fizycznymi dla obserwatorów O i O₁ należy współczynnik α zastąpić przez .

Równanie ruchu ciała, o masie m, w polu grawitacyjnym kuli o masie M wyznaczam tak, aby spełniało następujące warunki:

- równanie ruchu powinno być jednakowe dla każdego obserwatora spoczywającego względem kuli,

- przy niewielkim przesunięciu dla obserwatora O₁ ma postać

- dla lokalnego obserwatora O ma postać

Równanie ruchu ciała znajdującego się w punkcie O dla obserwatora O ma postać

Równanie ruchu ciała znajdującego się w punkcie O dla obserwatora O' można otrzymać podstawiając

do poprzedniego równania.

Ponieważ

więc ostatecznie dla O' równanie ruchu ciała znajdującego się w punkcie O ma postać

Weźmy punkt materialny P poruszający się blisko obserwatora O. Dla O₁ szukane równanie ma postać

gdzie czas t₁, pęd i siła działająca na punkt materialny są mierzone przez obserwatora O₁. Współczynnik α₁ jest obliczany dla miejsca gdzie znajduje się obserwator O₁, natomiast α jest powiązany z punktem materialnym (jest obliczany w miejscu gdzie aktualnie znajduje się punkt materialny P).

Jeżeli obserwator O₁ jest blisko obserwatora O, to

α₁ = α

i równanie przyjmie postać

i równocześnie

Dla niewielkich przesunięć ciała, w dowolnym miejscu przestrzeni, możemy uznać, że

i równanie ruchu możemy napisać, jako

Ponieważ dla obserwatora O₁, spoczywającego względem kuli α₁ = const., więc dla takiego obserwatora równanie ruchu ma postać

Tor ruchu jest taki sam dla każdego obserwatora, natomiast inne może być tempo upływu czasu lub przesunięcie ciała dla różnych obserwatorów.

Dla lokalnych ruchów możemy stosować II zasadę dynamiki Newtona, natomiast do ruchu w dużych obszarach przestrzeni należy stosować równanie

w którym pęd, czas i siła dla punktu materialnego znajdującego się w punkcie O są wyznaczane przez obserwatora O₁ pozostającego w spoczynku w polu grawitacyjnym kuli.

Dla obserwatora O', siła „przyciągania” działająca między ciałami o masach m' i M' znajdującymi się w odległości r', jest określona wzorem

Równanie ruchu punktu materialnego o masie m' w polu grawitacyjnym kuli o masie M' ma postać

;

wartość α jest obliczana w miejscu gdzie znajduje się punkt materialny.

Dla niewielkiego przesunięcia punktu materialnego o masie grawitacyjnej m_g i masie bezwładnej m mamy

Przyspieszenie a, z jakim porusza się ten punkt materialny, zależy od masy grawitacyjnej i masy bezwładnej tego punktu.

Masa bezwładna punktu materialnego jest określona wzorem

Jeżeli dwa ciała spadają swobodnie obok siebie z tymi samymi prędkościami, to niezależnie od wielkości ich mas spoczynkowych spadają z tym samym przyspieszeniem.

Jeżeli dwa ciała spadają swobodnie na Ziemię, to przechodząc przez ten sam punkt nad powierzchnią Ziemi mogą poruszać się z różnymi przyspieszeniami w zależności od ich prędkości. Ciała poruszające się szybciej mają większą masę bezwładną, przy tej samej masie grawitacyjnej.

Jeżeli v₁ < v₂ (m₁ < m₂), to a₁ > a₂.

Prędkość swobodnie spadającego ciała jest w każdej chwili mniejsza od prędkości światła.

W układzie inercjalnym pęd przekazywany przez grawitony oddziałujące z jednorodnym ciałem, w kształcie kuli, jest wektorem zerowym i energia przez nie przekazywana jest równa zero. Jeżeli na ciało nie działają zewnętrzne siły, to ciało porusza się ruchem jednostajnym i jego całkowita energia , dla ustalonego obserwatora O' jest stała. Również jego energia kinetyczna pozostaje stała.

Jeżeli w układzie inercjalnym obserwatora O' ciało zmieniło swoją prędkość, to jest to możliwe, zgodnie z Założeniem 5, jeżeli na ciało działa zewnętrzna siła . Siła jest potrzebna do zrównoważenia siły bezwładności powstałej w wyniku asymetrycznego oddziaływania ciała z grawitonami. Ciało zmienia swój pęd i energię kinetyczną dzięki pracy , wykonanej przez tą siłę. Ciało zmieniające swoją prędkość absorbuje i emituje tyle samo grawitonów, nie powiększa swojej energii wewnętrznej E_w i nie zmienia energii przestrzeni. Całkowita energia tego ciała, po zmianie prędkości, jest równa sumie całkowitej energii ciała przed zmianą prędkości i pracy .

Zmiana energii kinetycznej tego ciała jest równa .

Zewnętrzna siła działająca na ciało, znajdujące się w układzie inercjalnym, zmieniająca jego prędkość, powoduje zmianę jego energii całkowitej kosztem pracy tej siły. Ciało nie zmienia swojej energii wewnętrznej; następuje jedynie zmiana energii kinetycznej.

Jeżeli ciało nie jest kulą to jego ruch w układzie inercjalnym może wyglądać inaczej. Rozpatrzmy sytuację przedstawioną w podrozdziale 1.1. przedstawioną na rysunku 1.1.1.. Niech kule poruszają się w układzie UW. Kula znajdująca się w punkcie A' emituje w stronę punktu B wirtualne grawitony, które nie są absorbowane przez kulę B, nie przekazują do niej żadnego pędu i kula B nie jest hamowana. Analogicznie nie jest hamowana druga kula. Grawitony wirtualne emitowane przez przestrzeń i materię, poruszające się z prędkością światła, w stronę kuli B od strony kuli A' są absorbowane przez kulę A' i nie dochodzą do kuli B. W wyniku tego na kulę B działa siła F zwrócona w stronę A'. Analogicznie na kulę A działa siła F zwrócona w stronę kuli B'. Na układ dwóch kul działa wypadkowa siła 2F₁, która hamuje ich ruch, a więc zmniejsza ich pęd.

Zmiana pędu kul następuje w wyniku ich oddziaływania z cząstkami przestrzeni i materii za pośrednictwem grawitonów. Suma pędów przekazanych do kul przez grawitony jest wektorem przeciwnym do sumy pędów przekazanych przez te grawitony do cząstek przestrzeni i materii. Kule zmieniają swój pęd, ale pewne cząstki przestrzeni i cząstki pozostałej materii również odpowiednio zmieniają swój pęd. Zasada zachowania pędu jest zachowana, ponieważ całkowity pęd przekazany do cząstek kul oraz cząstek przestrzeni i materii jest wektorem zerowym.

W układzie nieinercjalnym, dla ustalonego obserwatora O', w różnych miejscach przestrzeni ilości grawitonów absorbowanych przez punkt materialny, w jednostce czasu, są na ogół różne i odpowiednio różne jego spoczynkowe energie wewnętrzne (masy grawitacyjne). Całkowita energia punktu materialnego jest funkcją jego położenia i prędkości w polu grawitacyjnym.

W polu grawitacyjnym materialnej kuli występuje asymetria ilości grawitonów absorbowanych przez punkt materialny z różnych kierunków przestrzeni. Ze względu na tą asymetrię suma pędów przekazanych temu punktowi przez grawitony z nim oddziałujące jest wektorem niezerowym, skierowanym do środka kuli.

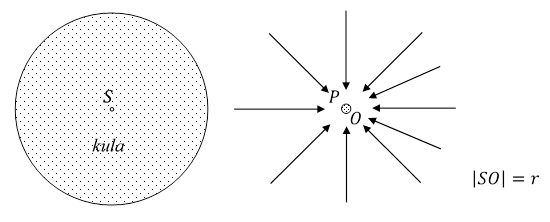
Rys. 3.4.2.

Z punktem materialnym P, znajdującym się w odległości r od środka S materialnej kuli, oddziałuje mniej grawitonów od strony kuli niż ze strony przeciwnej. Jeżeli punkt materialny jest nieruchomy względem kuli, to dla obserwatora O, znajdującego się blisko tego punktu, działa na ten punkt materialny siła

skierowana do środka kuli, gdzie jest sumą pędów przekazanych przez grawitony oddziałujące z punktem materialnym w czasie Δt. Punkt materialny puszczony swobodnie zaczyna spadać na kulę ruchem przyspieszonym w taki sposób, że zmiana jego pędu, w czasie Δt, jest równa sumie pędów przekazywanych temu punktowi materialnemu przez grawitony oddziałujące z nim w tym samym czasie. Energia kinetyczna spadającego punktu materialnego wzrasta, natomiast jego energia wewnętrzna maleje.

W przypadku ruchu swobodnego, w stronę przeciwną do środka kuli, punkt materialny zmniejsza swoją energię kinetyczną równocześnie zwiększając swoją energię wewnętrzną.

Jeżeli punkt materialny ma większą masę, to oddziałuje z nim więcej grawitonów i zmiana pędu jest wprost proporcjonalna do jego masy.

Część grawitonów oddziałujących ze spadającym swobodnie punktem materialnym powoduje zmianę jego pędu, suma pędów pozostałych jest wektorem zerowym. Dla obserwatora związanego ze spadającym punktem materialnym sytuacja jest taka, jak gdyby znajdował się w spoczynku w układzie inercjalnym.

Układ współrzędnych związany ze swobodnie spadającym ciałem jest układem lokalnie inercjalnym.

Weźmy materialną kulę o środku S i układ OXYZ pozostający w spoczynku względem kuli. Niech obserwator O₁, związany z prostokątnym układem współrzędnych O₁X₁Y₁Z₁, porusza się ruchem postępowym, tak jak swobodnie spadające ciało na powierzchnię materialnej kuli. Punkt materialny P znajduje się blisko obserwatora O₁.

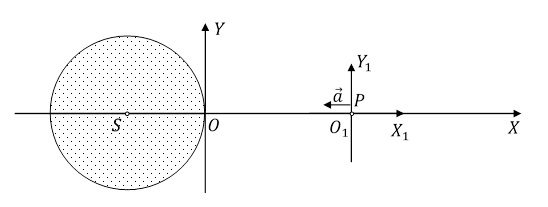
Rys. 3.4.3.

Niech punkt materialny P pozostaje początkowo w spoczynku w układzie O₁X₁Y₁Z₁. Dla obserwatorów O₁ i O z punktem materialnym oddziałują te same grawitony. Dla obserwatora O₁ suma pędów przekazanych przez grawitony oddziałujące z punktem materialnym jest wektorem zerowym (nie liczą się te grawitony, które zmieniają pęd punktu materialnego), natomiast dla obserwatora O jest wektorem niezerowym zmieniającym prędkość tego punktu. Dla obserwatora O₁ siła działająca na punkt P jest wektorem zerowym. Układ O₁X₁Y₁Z₁ jest układem lokalnie inercjalnym. Według obserwatora O część grawitonów oddziałujących z punktem materialnym zmienia jego pęd, natomiast pozostałe, których suma pędów jest wektorem zerowym, działają na niego siłą bezwładności. Dla obserwatora O na swobodnie spadający, w polu grawitacyjnym, punkt materialny działa zerowa siła bezwładności.

Jeżeli punkt P w układzie O₁X₁Y₁Z₁ będzie poruszał się tak, że dla obserwatora O pozostaje w spoczynku, wówczas działa na niego pewna siła. Dla obserwatora O₁ jest to siła bezwładności, natomiast dla obserwatora O jest to siła grawitacji, powstała ze względu na obecność kuli. Obydwie siły są skutkiem tego, że od strony przeciwnej do środka kuli z punktem materialnym oddziałuje więcej grawitonów niż od środka kuli. Jednak dla obserwatora O₁ mechanizm powstawania siły bezwładności, działającej na punkt materialny P, jest nieco inny niż w przypadku powstawania siły bezwładności w układzie inercjalnym. Nie występują grawitony, które są potrzebne do zmiany pędu w układzie O₁X₁Y₁Z₁, natomiast występują grawitony, których oddziaływanie z P wytwarza siłę bezwładności.

Jeżeli punkt materialny porusza się w inny sposób w układzie O₁X₁Y₁Z₁, to siła działająca na niego dla O₁ jest siłą bezwładności, natomiast dla O jest sumą siły grawitacji i siły bezwładności.

Układy lokalnie inercjalne znajdujące się w polu grawitacyjnym mogą poruszać się względem siebie ruchem przyspieszonym.

Grawitony oddziałujące z Układem Słonecznym, sąsiednimi gwiazdami i galaktykami można podzielić na dwie grupy (patrz 4.2.).

Pierwsza grupa grawitonów przekazuje niezerowy pęd i powoduje ruch przyspieszony, z tym samym przyspieszeniem, tych ciał, jako całości. Ten ruch odpowiada swobodnemu spadkowi w polu grawitacyjnym. Układ Słoneczny i jego otoczenie spada swobodnie w stronę przeciwną do środka Wszechświata.

Druga grupa grawitonów, możliwie największa, przekazuje w sumie zerowy pęd do tych ciał. Dlatego, dla obserwatora znajdującego się w pewnej odległości od najbliższych gwiazd układ odniesienia, w którym bliskie gwiazdy i galaktyki pozostają w spoczynku, jest układem niemal inercjalnym. Komplikację stanowi fakt ruchów własnych gwiazd i galaktyk w takim układzie, jednak w niezbyt długim okresie czasu zmiany ich położenia można pominąć.

Układ odniesienia związany z najbliższymi gwiazdami i galaktykami jest z dobrym przybliżeniem układem lokalnie inercjalnym (ULI).

Jeżeli ciało porusza się ruchem jednostajnym na powierzchni Ziemi w układzie pozostającym w spoczynku względem ULI, to druga grupa grawitonów z nim oddziałująca przekazuje mu zerowy pęd i na ciało nie działa żadna siła (pomijając siłę grawitacji).

Jeżeli ciało porusza się ruchem przyspieszonym, to działa na niego siła bezwładności, ponieważ część grawitonów drugiej grupy jest potrzebna do zmiany pędu tego ciała.

Jeżeli ciało wykonuje ruch obrotowy w ULI, to na jego cząstki działa siła odśrodkowa, ponieważ te cząstki poruszają się ruchem przyspieszonym w tym układzie i następuje zmiana ich pędu.

Sąsiednie gwiazdy i galaktyki określają jedynie układ ULI, ale nie mają wpływu na wartość siły bezwładności czy siły odśrodkowej. O wartości siły bezwładności decyduje oddziaływanie grawitacyjne ciała z wszystkimi cząstkami przestrzeni Wszechświata zawartymi w kuli oddziaływania grawitacyjnego.

W doświadczeniu Newtona z wiadrem woda wykonuje ruch obrotowy w układzie ULI związanym z sąsiednimi gwiazdami i galaktykami.

Ruch ciał w Układzie Słonecznym odbywa się względem strumienia grawitonów drugiej grupy dochodzących do tego Układu, emitowanych przez cząstki przestrzeni znajdujące się w kuli oddziaływania grawitacyjnego. Środkiem tej kuli jest Układ Słoneczny. Ruch przyspieszony ciała w układzie ULI powoduje asymetrię ilości grawitonów drugiej grupy oddziałujących z nim z różnych kierunków przestrzeni. Dla ruchu jednostajnego oddziaływanie jest symetryczne.

Dla obserwatora O' masa bezwładna ciała m' zmienia się w zależności od prędkości ciała, jak również od jego położenia względem innych ciał. W skład bezwładnej masy ciała wchodzą również składniki odpowiadające energii kinetycznej oraz energii potencjalnej ciała. Energia potencjalna materialnego ciała jest pewną częścią energii wewnętrznej ciała.

Masę bezwładną poruszającego się ciała obserwator O' może wyznaczyć w następujący sposób. Najpierw masę ciała ustala obserwator O znajdujący się w pobliżu poruszającego się ciała,

gdzie jest masą spoczynkową poruszającego się ciała, v jest prędkością tego ciała względem O. Obserwator O' mnoży masę m_v przez α i otrzymuje masę m'.

Czynnik

jest taki sam dla obydwu obserwatorów.

Jak widać obserwator O' może również wyznaczyć bezpośrednio masę ciała dzieląc masę ciała , wyznaczoną przy pomocy własnego zegara, przez

Między masą bezwładną ciała i jego energią całkowitą zachodzi związek

E = mc²,

przy czym ten wzór ma charakter lokalny, to znaczy jest prawdziwy tylko dla ciał znajdujących się blisko obserwatora O, który mierzy energię E i masę m. Dla obserwatora O' znajdującego się daleko od O i innych ciał materialnych mamy zależność

E' = m'c'²,

gdzie

c' = cα².

W przybliżeniu podczas swobodnego spadku punktu materialnego na kulę, dla dowolnego ustalonego obserwatora O, nie zmienia się masa ciała. Ponieważ

m = const.,

więc dla swobodnie spadającego ciała

Jeżeli masa swobodnie spadającego ciała jest stała, to dla dowolnego obserwatora

Stosując przybliżone rachunki otrzymujemy

W ten sposób otrzymujemy klasyczną postać zasady zachowania energii dla swobodnie spadającego ciała.

Ruch ciała jest ruchem jego cząstek elementarnych. Ruch cząstki elementarnej nie jest ciągły, ale skokowy. Pęd i energia cząstki elementarnej, podczas jej spoczynku w układzie UW, zmieniają się również skokowo w wyniku jej oddziaływania z grawitonami. Dlatego kierunki i długości skoków cząstki elementarnej, w niewielkim stopniu, zmieniają się w sposób przypadkowy. Również zmiana pędu ciała jest nieciągła. Jednak w zwykłych warunkach zmiana pędu ciała wydaje się ciągła, ze względu na bardzo dużą ilość oddziaływań cząstek elementarnych ciała z grawitonami, podczas których grawiton przekazuje, na ogół, niewielki pęd. Jednak podczas ruchu cząstki elementarnej lub ciała złożonego z niewielkiej ich ilości należy uwzględniać efekty kwantowego oddziaływania z grawitonami.

Weźmy obserwatora O znajdującego się w początku układu współrzędnych OXYZ. Jeżeli obserwator O zapali lampę, to czoło fali świetlnej jest sferą określoną równaniem

x² + y² + z² - c²t² = 0.

Dla obserwatora O' po przeniesieniu początku układu współrzędnych O'X'Y'Z' do punktu O, x' = xα, y' = yα, z' = zα, , c' = cα² i równanie czoła fali ma postać

Również dla O' czoło fali świetlnej jest sferą.

Weźmy obserwatora O' spoczywającego względem pewnego układu ciał materialnych i znajdującego się daleko od nich. Obserwator O, wraz ze swoim materialnym otoczeniem, może zmieniać położenie względem tych ciał.

Obserwator O' może zauważyć pewne zmiany zachodzące w otoczeniu obserwatora O. Mogą zmieniać się: tempo upływu czasu, masa i energia wewnętrzna cząstek elementarnych, rozmiary cząstek i odległości między nimi, prędkość światła i oddziaływanie grawitacyjne między ciałami.

Natomiast obserwator O nie zauważy żadnej z tych zmian w ciałach znajdujących się blisko niego i pozostających względem niego w spoczynku. Obserwator O podlega tym samym zmianom co jego otoczenie i dla niego żadne zmiany nie zachodzą.

Te zmiany zachodzą w rzeczywistości a nie są wynikiem wybranego sposobu mierzenia odległości, czasu czy innych wielkości fizycznych.