1.9. Oddziaływanie grawitacyjne między materią lub przestrzenią zawartą w elementach objętości

Założenie 6.
Objętość Wszechświata jest skończona.
Z materią oraz przestrzenią zawartą w elemencie objętości ΔV, w czasie Δt, oddziałuje skończona ilość grawitonów.
Wszechświat jest kulą zawierającą, w bardzo dużej skali, równomiernie rozmieszczone cząstki materii i przestrzeni; średnia gęstość materii jest równa średniej gęstości przestrzeni
.
Średnia łączna gęstość materii i przestrzeni
.

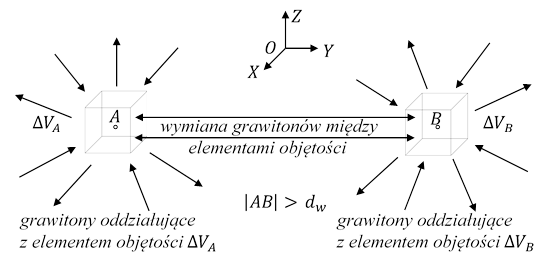
Rys. 1.9.1.

Cząstki materii oraz przestrzeni w elemencie ΔV_A oddziałują z cząstkami materii oraz przestrzeni w elemencie ΔV_B.

Założenie 7.
Weźmy w prostokątnym układzie współrzędnych OXYZ dowolne elementy objętości ΔV_A i ΔV_B o środkach w punktach przestrzeni A i B takich, że |AB| > d_w. Masa materii i masa przestrzeni w elemencie ΔV_A oraz masy i w elemencie ΔV_B są określone przez dowolnego ustalonego obserwatora O, znajdującego się w początku układu OXYZ, przy pomocy własnego zegara Z.
Ilość grawitonów oddziałujących, w czasie Δt, z materią zawartą w elemencie objętości ΔV_A, które są emitowane lub absorbowane przez materię zawartą w elemencie objętości ΔV_B jest wprost proporcjonalna do masy cząstek materii zawartych w elemencie ΔV_B, do masy materii w elemencie objętości ΔV_A i odwrotnie proporcjonalna do odległości |AB|.
Ilość grawitonów oddziałujących, w czasie Δt, z materią zawartą w elemencie objętości ΔV_A, które są emitowane lub absorbowane przez przestrzeń zawartą w elemencie objętości ΔV_B jest wprost proporcjonalna do masy cząstek przestrzeni zawartych w elemencie ΔV_B, do masy materii w elemencie objętości ΔV_A i odwrotnie proporcjonalna do odległości |AB|.
Współczynnik a_w jest taki sam dla każdego obserwatora pozostającego w spoczynku względem układu OXYZ.
Przyjmuję, w przybliżeniu, że odległość dwóch punktów w przestrzeni, obliczana przez ustalonego obserwatora, jest równa ich odległości w prostokątnym układzie współrzędnych.

Odległość dwóch punktów w przestrzeni jest omówiona w Rozdziale II, podrozdział 2.5..

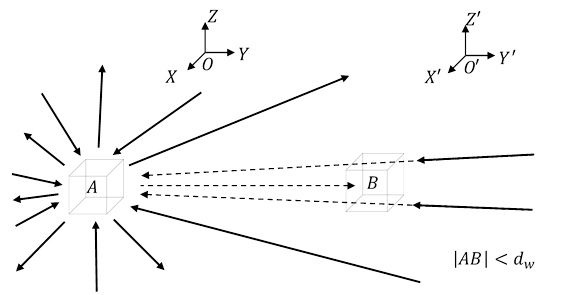
Rys. 1.9.2.

Ze względu na obecność materii w elemencie ΔV_B, ilość grawitonów oddziałujących między cząstkami przestrzeni oraz cząstkami materii znajdującymi się w całym Wszechświecie i cząstkami materii w elemencie ΔV_A jest mniejsza, niż gdyby w elemencie ΔV_B nie było cząstek materii. Zmniejszenie ilości grawitonów zależy od odległości elementu A od B.

Założenie 8.
Jeżeli |AB| < d_w, to ilość grawitonów obliczanych dla całej materii i przestrzeni Wszechświata (poza materią zawartą w elementach ΔV_A i ΔV_B), które nie oddziałują, w czasie Δt, z materią zawartą w elemencie objętości ΔV_A, ze względu na obecność materii w elemencie objętości ΔV_B, jest wprost proporcjonalna do masy materii w elemencie objętości ΔV_B, do masy materii w elemencie objętości ΔV_A i odwrotnie proporcjonalna do odległości |AB|.
Współczynnik k_w jest taki sam dla każdego obserwatora pozostającego w spoczynku względem układu OXYZ. Wielkości występujące w Założeniach 8 i 9 mogą być mierzone przez dowolnego innego obserwatora O' znajdującego się w początku prostokątnego układu współrzędnych O'X'Y'Z' przy pomocy własnego zegara Z'.

Od strony elementu ΔV_B, ze wzglądu na obecność materii w tym elemencie, z materią w elemencie ΔV_A oddziałuje mniej grawitonów niż ze strony przeciwnej.

Ilość grawitonów, które nie oddziałują z materią zawartą w elemencie ΔV_B, ze względu na obecność materii w elemencie ΔV_A, jest określona wzorem

powstałym przez zamianę liter A i B. Stąd wynika

Ilość grawitonów, które nie oddziałują z materią zawartą w elemencie ΔV_A, ze względu na obecność materii w elemencie ΔV_B, jest taka sama, jak ilość grawitonów, które nie oddziałują z materią zawartą w elemencie ΔV_B, ze względu na obecność materii w elemencie ΔV_A, niezależnie od tego, jakie ilości materii są zawarte w tych elementach objętości.

Cząstka elementarna emituje ogromne ilości grawitonów, które są bardzo słabo pochłaniane przez elementarne cząstki materii oraz przestrzeni. Dlatego strumień grawitonów może przebyć bardzo duże odległości bez istotnego zmniejszenia jego natężenia, jeżeli gęstość materii i przestrzeni nie jest zbyt duża. Dopiero bardzo gęsta materia w gwieździe neutronowej zmniejsza jego natężenie w większym stopniu.

Założenia 7 i 8 są konsekwencją przedstawionego w podrozdziale 1.7. oddziaływania grawitacyjnego między elementarnymi cząsteczkami materii i przestrzeni; nowym istotnym elementem tych założeń jest niezależność współczynników k_w i a_w od obserwatora. Ilości grawitonów oddziałujących lub nieoddziałujących między cząsteczkami są odwrotnie proporcjonalne do odległości między elementami objętości, w których znajduje się materia lub przestrzeń. Przy takim założeniu, zmiana masy (energii wewnętrznej) ciała, przy przesunięciu w polu grawitacyjnym, jest równoważna zmianie energii potencjalnej tego ciała i zarazem pracy siły równoważącej siłę grawitacji przy takim przesunięciu. Zostało to pokazane w podrozdziale 2.3..

Oddziaływanie grawitacyjne między ciałami jest sumą oddziaływań między elementarnymi cząstkami materii i przestrzeni, które mają niewielkie rozmiary. Wobec bardzo małych rozmiarów cząstek elementarnych wzory występujące w tych założeniach są poprawne do odległości rzędu rozmiarów atomów.

[k_w] = ms

Ponieważ

więc

Weźmy dwóch obserwatorów O i O'. Dla każdego obserwatora grawiton oddziałuje z cząstką lub nie. Niech dla obserwatora O, w czasie Δt, z materią w elementach ΔV_A i ΔV_B> oddziałuje odpowiednio ΔN_A i ΔN_B grawitonów oraz z materią w elemencie ΔV_A nie oddziałuje grawitonów. Dla obserwatora O' dla tych samych wartości ΔN_A, ΔN_B i upłynie czas Δt'. Dla obserwatorów O i O' odległości między elementami ΔV_A i ΔV_B są odpowiednio równe |AB| i |A'B'|.

Dla obserwatorów O i O' współczynnik k_w jest odpowiednio równy

Współczynnik k_w oraz a_w jest taki sam dla każdego obserwatora, gdy jest spełniony warunek

|AB|Δt i |A'B'|Δt'.

Ponieważ

więc wzór występujący w Założeniu 8 daje taką samą wartość liczbową dla każdego obserwatora.

Jeżeli r > d_w, to grawitony oddziałujące między materią zawartą w elementach ΔV_A i ΔV_B nie zmieniają masy materii znajdującej się w tych elementach. Ilość grawitonów emitowanych przez materię z elementu ΔV_A i absorbowanych przez materię zawartą w elemencie ΔV_B jest równa ilości grawitonów emitowanych przez materię z elementu ΔV_B i absorbowanych przez materię zawartą w elemencie ΔV_A. Dzięki temu energia wewnętrzna materii w tych elementach nie zmienia się ze względu na oddziaływanie grawitacyjne między tymi elementami.

Ze względu na obecność materii w elemencie objętości ΔV_B do materii zawartej w elemencie objętości ΔV_A jest przekazywany niezerowy pęd o zwrocie od A do B.

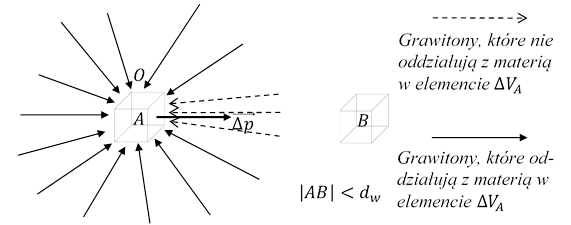
Rys. 1.9.3.

Założenie 9.
Niech |AB| < d_w. Grawitony, które ze względu na obecność materii w elemencie objętości ΔV_B (oznaczenia takie jak w Założeniu 9) nie oddziałują, w czasie Δt, z materią zawartą w elemencie objętości ΔV_A, nie przekażą pewnego pędu materii w elemencie ΔV_A. Pęd, który nie przekażą te grawitony do elementu ΔV_A, dla obserwatora O znajdującego się blisko elementu ΔV_A, jest równy
,
gdzie h jest stałą Plancka.
Współczynnik a_w jest taki sam dla każdego obserwatora pozostającego w spoczynku względem układu OXYZ.

Nie biorę pod uwagę pędu nieprzekazanego do elementu ΔV_A ze względu na przestrzeń zawartą w elemencie ΔV_B, ponieważ ma bardzo małą wartość.

Założenie 9 jest konsekwencją przedstawionego w podrozdziale 1.7. oddziaływania grawitacyjnego między elementarnymi cząstkami materii.

Niech grawitony oddziałujące z materią w elemencie ΔV_A przekazują do niej zerowy pęd, gdy w elemencie ΔV_B nie ma materii.

Ze względu na obecność materii w elemencie ΔV_B grawitony oddziałujące z materią, zawartą w elemencie ΔV_A, przekażą materii w tym elemencie pęd

Zwrot przekazanego pędu jest od punktu A do B.

gdzie G jest stałą grawitacji.