5.2. Ruch planety dookoła Słońca
Pierwszy sposób wyznaczania orbity planety.
Dla obserwatora O', znajdującego się daleko od Słońca, planety i innych ciał materialnych, masa planety i tempo upływu czasu zależą od miejsca przestrzeni, w którym te wielkości są mierzone. Ruch planety dookoła Słońca jest swobodnym spadkiem jednego ciała na drugie wobec tego dla obserwatora O' ich masy pozostają stałe. Pędy tych ciał zmieniają się w zależności od odległości r między nimi. Ruch planety wyznacza obserwator O' w układzie O'X'Y'Z'. Dla uproszczenia zapisu układ O'X'Y'Z' został przesunięty tak, że pokrywa się z układem S'X'Y'Z'. Stąd jednostki długości na osiach układu S'X'Y'Z' są takie same jak dla układu O'X'Y'Z'. Niech m' i M' oznaczają odpowiednio masę grawitacyjną planety ![]() i masę Słońca
i masę Słońca ![]() , mierzone przez obserwatora O'. Masa bezwładna planety
, mierzone przez obserwatora O'. Masa bezwładna planety
![]() ,
,
gdzie
![]() .
.
Ruch planety jest jej swobodnym spadkiem na Słońce, dlatego ![]() .
.
Prędkość planety jest stosunkowo niewielka i możemy przyjąć ![]() .
.
Dla planety Merkury β = 1 - 1,4⋅10-8. Dla pozostałych planet β jest jeszcze bliższa liczbie jeden.
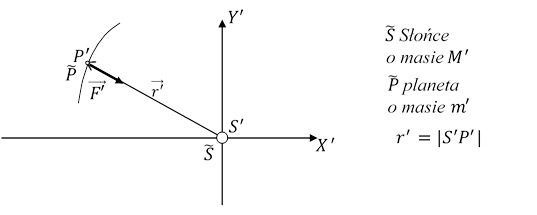
Rys. 5.2.1.
Równanie ruchu planety w układzie S'X'Y'Z', ma postać (patrz 3.4.)
![]() .
.
Współczynnik
![]()
i
![]() .
.
Ponieważ ![]() jest dla planety wielkością stałą, więc równanie ma postać
jest dla planety wielkością stałą, więc równanie ma postać
![]()
![]()
Współczynnik β jest bardzo bliski jeden. W dalszym ciągu przyjmuję β = 1.
![]()
Dla uproszczenia zapisu zamiast t', r', w', M' będę pisał odpowiednio t, r, w, M.
![]()
![]()
![]()
We współrzędnych kartezjańskich ruch planety dookoła Słońca wyznacza rozwiązanie x = x(t), y = y(t) układu równań różniczkowych.
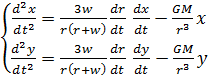
Po pomnożeniu pierwszego równania przez -y oraz drugiego przez x i dodaniu stronami otrzymujemy równanie.
![]()
![]()
We współrzędnych biegunowych x = r cos φ, y = r sin φ.
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Stała P jest w przybliżeniu podwojoną prędkością polową planety.
Układ równań
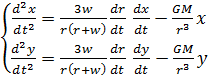
mnożymy odpowiednio przez ![]() oraz
oraz ![]() i dodajemy stronami.
i dodajemy stronami.
![]()
![]()
Dla współrzędnych biegunowych
![]()
oraz
x2 + y2 = r2.
Wprowadźmy oznaczenie
![]() .
.
![]()
![]()
![]()
Otrzymujemy równanie liniowe
![]() .
.
Rozwiązujemy równanie jednorodne
![]() .
.
![]()
![]()
![]()
Uzmienniamy stałą i rozwiązujemy równanie liniowe niejednorodne.
![]()
![]()
![]()
![]()
![]()
![]()
Pomijam wyraz
![]()
i następne, jako bardzo małe.
![]()
![]()
Rozwiązanie ma postać
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Podstawmy
![]() ,
,
![]() .
.
![]()
![]()
Odpowiednie równanie w teorii Newtona ma postać
![]() .
.
![]()
Oznaczmy
![]() .
.
Dla orbity newtonowskiej q = 1 .
![]()
Szukam rozwiązania tego równania w postaci u = a + b cos qφ .
![]()
![]()
L = b2q2 - b2q2 cos2 qφ
![]()
Funkcja u = a + b cos qφ jest rozwiązaniem równania
![]() ,
,
jeżeli są spełnione następujące warunki
![]()
i
![]() .
.
Rozwiązując układ otrzymujemy
![]()
i
![]() .
.
![]()
![]()

Oznaczmy
![]()
i
![]() .
.
Wówczas
![]() .
.
Kolejne minima funkcji r(φ) będą w odstępie Δφ takim, że qΔφ = 2π.
![]()
![]()
![]()
Obliczone przesunięcie peryhelium planety ![]() .
.
Rzeczywista orbita planety niewiele odbiega od orbity obliczonej na podstawie prawa Newtona. Z III prawa Keplera
![]()
i wzoru na pole elipsy
![]()
otrzymujemy
![]() ,
,
gdzie
![]()
jest kwadratem prędkości polowej, a dużą półosią natomiast e mimośrodem elipsy. Kwadrat podwojonej prędkości polowej P2 = GMa(1 - e2).
![]()
![]() w = 1476,69 m
w = 1476,69 m
| Merkury | Wenus | Ziemia | |
| a | 5,7909⋅1010 m | 1,0821⋅1011 m | 1,4960⋅1011 m |
| e | 0,2056 | 0,0068 | 0,0167 |
| T | 0,2408 roku | 0,6152 roku | 1 rok |
| ε | 5,0188⋅10-7 rad / orbita 42,99" /stulecie | 2,5724⋅10-7 rad / orbita 8,62" /stulecie | 1,8611⋅10-7 rad / orbita 3,84" /stulecie |
| ε obs. astr | 43,11 ± 0,45" / stulecie | 8,4 ± 4,8" / stulecie | 5,0 ± 1,2" / stulecie |
Obliczone przesunięcia peryhelium są zgodne z wartościami uzyskanymi z obserwacji astronomicznych i są takie same jak w OTW.
Prędkość polowa planety nie jest stała. Określa ją wartość wyrażenia
![]() ,
,
gdzie P jest wartością stałą. Prędkość polowa planety w niewielkim stopniu zależy od jej odległości od Słońca.
Różnica prędkości polowej dla aphelium i peryhelium jest równa
![]() .
.
Ponieważ
![]()
oraz
![]()
są bliskie zera, więc
![]() .
.
![]()
Dla planety Merkury
![]() ,
,
![]()
i
![]() .
.
Obliczone równanie orbity planety ma postać

i
![]() .
.
![]()
Dla orbity newtonowskiej mamy
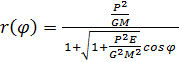 .
.
![]()
Drugi sposób wyznaczania orbity planety.
Energia kinetyczna planety jest określona wzorem
![]() .
.
![]()
![]()
![]() .
.
Energię potencjalną określam wzorem
![]()
![]() .
.
![]() .
.
Lagrangian ma postać
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Równania Lagrangea
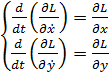
mają postać
![]()
![]()
Równania mnożymy odpowiednio przez -y i x i dodajemy stronami.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We współrzędnych biegunowych x = r cos φ, y = r sin φ.
![]()
![]()
![]()
![]()
Stała P jest w przybliżeniu podwojoną prędkością polową planety.
Równania Lagrangea mnożymy odpowiednio przez ![]() i
i ![]() i dodajemy stronami.
i dodajemy stronami.

![]()
![]()
![]()
![]()
Oznaczmy ![]() . Dla współrzędnych biegunowych
. Dla współrzędnych biegunowych
![]()
oraz
x2 + y2 = r2.
![]()
Rozwiązujemy równanie jednorodne
![]() .
.
![]()
![]()
![]()
Uzmienniamy stałą K i rozwiązujemy równanie liniowe niejednorodne.
![]()
![]()
![]()
![]()
![]()
![]()
Rozwiązanie ma postać
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Podstawmy
![]() ,
,
![]() .
.
![]()
![]()
![]()
![]()
![]()
Wartość ![]() jest bliska zera.
jest bliska zera.
![]()
Otrzymaliśmy takie samo równanie jak w pierwszym przypadku.
Jednak prędkość polowa planety nie jest stała i jest określona innym wzorem niż w pierwszym przypadku. Określa ją wartość wyrażenia
![]()
![]() ,
,
gdzie P jest wartością stałą. Prędkość polowa planety w niewielkim stopniu zależy od jej odległości od Słońca.
Różnica prędkości polowej dla aphelium i peryhelium jest równa
![]() .
.
Ponieważ
![]()
oraz
![]()
są bliskie zera, więc
![]() .
.
![]()
Dla planety Merkury
![]() ,
,
![]()
i
![]() .
.