2.1. Zmiana masy punktu materialnego przy jego przesunięciu w polu grawitacyjnym materialnej kuli
Weźmy jednorodną materialną kulę o gęstości 
, objętości 
, masie 
, promieniu d i środku S oraz punkt materialny P.
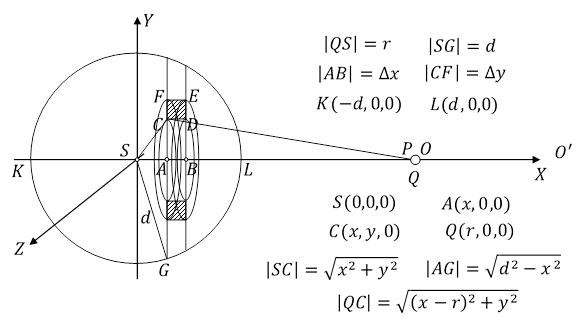
Rys. 2.1.1.
Daleko od kuli i innych ciał materialnych znajduje się obserwator O', który nie zmienia swojego położenia w układzie SXYZ. Początkowo punkt materialny P był umieszczony obok obserwatora O' i jego masa wyznaczona przez tego obserwatora jest równa 
. Następnie ten punkt materialny umieszczono w punkcie Q, w odległości r od środka S kuli tak, że d < r < dw i jego masa wyznaczona przez obserwatora O' jest 
. Masa jest mniejsza od masy 
, ponieważ z punktem materialnym oddziałuje mniej grawitonów ze względu na obecność materialnej kuli, przy zachowaniu tych samych jednostek czasu.
Zakładam, że masa punktu materialnego jest bardzo mała w stosunku do masy kuli, kula i punkt materialny są w spoczynku w układzie SXYZ, oraz że punkt materialny P i kula znajdują się w bardzo dużej odległości od innych ciał materialnych. Wielkości primowane są mierzone przez obserwatora O', natomiast nieprimowane są mierzone przez obserwatora O, znajdującego się blisko punktu Q.
Obliczmy ilość grawitonów ΔN, które nie oddziałują z punktem materialnym P ze względu na obecność kuli. Ponieważ, dla odpowiednich elementów odległości i odpowiednich odstępów czasu, ΔN jest takie samo dla każdego obserwatora, to możemy zamiast O' wybrać obserwatora O.
Weźmy pierścień kołowy utworzony przez obrót prostokąta CDEF dookoła osi OX. Objętość tego pierścienia
ΔV = 2πyΔyΔx.
Obecność materii w pierścieniu zmniejsza ilość grawitonów oddziałujących z punktem materialnym P. Zmniejszenie ΔNp ilości grawitonów oddziałujących z punktem materialnym P, w czasie Δt, jest wprost proporcjonalne do masy
materii zawartej w tym pierścieniu, do masy punktu materialnego 
zmierzonej przez O (
na podstawie Założenia 5), do czasu Δt i odwrotnie proporcjonalne do odległości |QC| elementów pierścienia od punktu P.
Łączną ilość tych grawitonów, które nie oddziałują z punktem materialnym ze względu na obecność materii w kuli, określa wzór
Wprowadźmy chwilowe oznaczenie
.
Do pierwszej całki zastosujemy podstawienie
d2 + r2 - 2rx = t,
,
.
Górną granicę całkowania należy zmienić na
d2 - 2rd + r2 = (r - d)2
a dolną na
d2 + 2rd + r2 = (r + d)2.
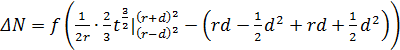
Zmniejszenie ilości grawitonów oddziałujących z punktem materialnym jak również z kulą, dla obserwatora O, jest równe
.
Ta zmiana nie zależy od promienia kuli.
Zmiana masy punktu materialnego, dla obserwatora O, jest
.
Dla obserwatora O' zmniejszenie ilości grawitonów oddziałujących z punktem materialnym jest
.
Stąd wynika, że masa punktu materialnego, dla obserwatora O', zostanie zmniejszona o
.
m' i mk' są masami punktu materialnego i kuli, gdy te ciała znajdują się w odległości r' < dw'. Są mniejsze od ich mas, gdy ciała znajdowały się daleko od siebie i innych mas.
Masa punktu materialnego dla O' jest równa
.
Dla obserwatora O masa punktu materialnego jest równa m. Zgodnie z Założeniem 5 m = m0'.
dla
Ponieważ z punktem materialnym P w czasie Δt' oddziałuje mniej grawitonów, ze względu na obecność kuli, więc, dla obserwatora O', masa m' jest mniejsza w porównaniu z masą m wyznaczoną przez obserwatora O.
Oznaczmy przez Nk ilość grawitonów, które oddziałują z kulą w czasie Δt' dla obserwatora O' i zarazem w czasie Δt dla obserwatora O.
Wówczas
.
Współczynnik
nie zależy od wyboru obserwatora.
m' = mα
Masę m mierzy obserwator O i m' jest wartością tej masy dla obserwatora O' określoną przy pomocy układu jednostek obserwatora O.
Jeżeli
r > dw,
to
m' = m.
Dla punktu materialnego leżącego wewnątrz kuli ilość tych grawitonów, które nie oddziałują z punktem materialnym ze względu na obecność materii w kuli określa ten sam wzór, jak i dla punktu leżącego na zewnątrz. Należy tylko uwzględnić, że r < d.
Dla punktu materialnego leżącego na powierzchni kuli zmniejszenie masy jest równe
.
Jeżeli punkt materialny jest w środku kuli, to zmniejszenie masy jest
.
Dla obserwatora O' masa m' punktu materialnego znajdującego się wewnątrz materialnej kuli jest równa
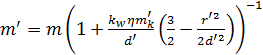
dla
.
Podczas przesunięcie punktu materialnego z O' do O, dla obserwatora O', masa kuli zmniejsza się od wartości 
do 
, o taką samą wartość, o jaką zmniejsza się masa punktu materialnego,
.
Stąd otrzymujemy
.
Jeżeli masa punktu materialnego jest bardzo mała w stosunku do masy kuli, to z bardzo dobrym przybliżeniem możemy przyjąć, że dla obserwatora O' masa kuli podczas tego przesunięcia jest stała,
.
Grawitony wirtualne przechodzące przez materię o małej gęstości są bardzo słabo pochłaniane. Jeżeli gęstość materii kuli nie jest zbyt duża, to strumień grawitonów wirtualnych dochodzących do każdego elementu objętości kuli jest niemal taki sam. Możemy uznać, w tym przypadku, że gęstość materii kuli w dowolnym elemencie objętości nie zależy od jego położenia w kuli.
Zmniejszenie ilości grawitonów oddziałujących z punktem materialnym P, ze względu na materię zawartą w tym elemencie, może być obliczone zgodnie z Założeniem 8 tylko do pewnej gęstości materii kuli (przypuśćmy do gęstości materii w gwieździe neutronowej 
). Przy wyprowadzaniu wzoru
zakładałem, że gęstość materii dla każdego elementu objętości jest jednakowa.
Powyższy wzór jest również prawdziwy, gdy gęstość materii kuli zależy jedynie od odległości od środka kuli.
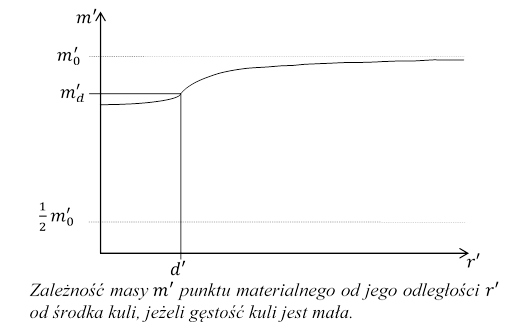
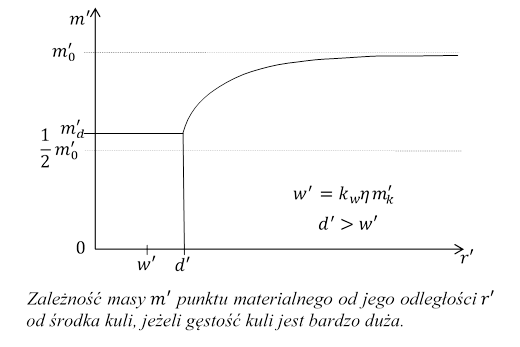
Dla większej gęstości materii kuli strumień grawitonów dochodzących do punktu P i przechodzący przez kulę w znacznie większym stopniu zmniejsza swoje natężenie niż w przypadku kuli o mniejszej gęstości. Ilość grawitonów absorbowanych przez punkt materialny P, znajdujący się na zewnątrz kuli, niezależnie od jej gęstości, może zmniejszyć się najwyżej do połowy (grawitony byłyby absorbowane tylko z jednej strony punktu P). Równocześnie masa może się zmniejszyć najwyżej do połowy.
Stąd otrzymujemy
.
W przypadku dużej gęstości materii kuli wzór
może być stosowany, jeżeli 
i 
.
