1.6. Masa elementarnej cząstki materii lub przestrzeni oraz ciała złożonego z cząstek

Cząstki elementarne nie są tworem statycznym. W każdej sekundzie z cząstką oddziałuje ogromna ilość grawitonów, emitowanych i absorbowanych przez nią. Elementarna cząstka materii lub przestrzeni jest obiektem wypełnionym energią, której ilość może się zmieniać w wyniku jej wymiany z innymi cząstkami za pośrednictwem grawitonów. Cząstkę elementarną możemy sobie wyobrazić, jako wrzącą kulę energii o bardzo małym promieniu, nieustannie emitującą oraz absorbującą grawitony w ogro­mnych ilościach (jest to uproszczone spojrzenie na cząstkę tylko ze względu na oddziaływanie grawitacyjne).

Grawitony absorbowane przez cząstkę, w czasie Δt, zwiększają zawartą w niej energię o ΔE_a (masę o ) natomiast grawitony emitowane, w tym czasie, zmniejszają jej energię o (masę o ).

Energia wewnętrzna (masa) cząstki elementarnej jest wprost proporcjonalna do ilości grawitonów przez nią absorbowanych i równocześnie do ilości energii przekazywanej do niej przez te grawitony, w jednostce czasu.

Różne rodzaje cząstek elementarnych w tym samym odstępie czasu mogą absorbować inną ilość grawitonów, dlatego różnią się ilością energii wewnętrznej (masą).

Masa* grawitacyjna cząstki (materii lub przestrzeni) oraz ciała złożonego z cząstek, dla ustalonego obserwatora O, jest równa ilości grawitonów oddziałujących (absorbowanych i emitowanych) z cząstkę lub ciałem w jednostce czasu, odmierzanej przez zegar obserwatora Δt.

Tak zdefiniowaną masę grawitacyjną będę oznaczał symbolem m*. Masa m* ciała jest miarą jego oddziaływania z cząstkami materii i przestrzeni zawartymi we Wszechświecie w odległości większej niż d_w = 10 ²⁴ m od tego ciała.

N oznacza ilość grawitonów oddziałujących z cząstkę lub ciałem, w czasie Δt. Wymiarem tak określonej masy m* jest .

W ustalonych warunkach ilość grawitonów absorbowanych przez cząstkę, w jednostce czasu, jest stała. Między ilością grawitonów absorbowanych a ilością grawitonów emitowanych przez cząstkę, w jednostce czasu, ustala się równowaga; ilość grawitonów emitowanych przez cząstkę jest równa ilości grawitonów przez nią absorbowanych. Dlatego ilość energii wewnętrznej (masa*) cząstki jest niemal stała. Ponieważ grawitony są absorbowane i emitowane w przypadkowych chwilach czasu, więc w bardzo małych odstępach czasu masa* cząstki może się zmieniać, oscylując wokół pewnej średniej wielkości ustalonej w dłuższym odstępie czasu. Masa* cząstki, w krótkich odstępach czasu, zmienia się w niewielkim stopniu w sposób chaotyczny.

Jeżeli zmniejszy się ilość grawitonów absorbowanych przez cząstkę, wówczas odpowiednio zmniejszy się ilość grawitonów przez nią emitowanych. Zmaleje energia wewnętrzna cząstki i zarazem jej masa* odpowiednio do ilości absorbowanych grawitonów. Część energii wewnętrznej cząstki zostanie przekazana do cząstek przestrzeni i innych cząstek materii, za pośrednictwem grawitonów, lub zostanie zamieniona na pracę lub energię.

Jeżeli zwiększy się ilość grawitonów absorbowanych przez cząstkę, wówczas odpowiednio zwiększy się ilość grawitonów przez nią emitowanych. Wzrośnie jej energia wewnętrzna i zarazem masa* odpowiednio do ilości absorbowanych grawitonów. Cząstka pobierze pewną ilość energii z cząstek przestrzeni i innych cząstek materii, za pośrednictwem grawitonów.

Energia wewnętrzna cząstki może się również powiększyć kosztem pracy wykonanej przez zewnętrzną siłę lub przez zamianę energii kinetycznej na wewnętrzną.

Zmiana masy* elementarnej cząstki jest możliwa dzięki nieustannej wymianie energii między tą cząstką i innymi elementarnymi cząstkami materii i przestrzeni. Gdyby do cząstki nie dochodziły grawitony z zewnątrz, to cząstka wyemitowałaby całkowicie swoją energię i jej masa byłaby równa zero. Wynika stąd następujący wniosek.

Cząstka elementarna jest obiektem zbudowanym, w znacznym stopniu, z energii.

Jak wiadomo ze Szczególnej Teorii Względności energia wewnętrzna cząstki jest równa E_w = mc².

Masa grawitacyjna m* cząstki, podobnie jak ładunek elektryczny, nie zależy od ruchu tej cząstki względem obserwatora O, ponieważ cząstka oddziałuje z grawitonami tylko podczas spoczynku w układzie UW. Masa grawitacyjna cząstki jest równa jej masie spoczynkowej.

Jeżeli elementarna cząstka o promieniu d i polu powierzchni S = 4πd², znajduje się daleko od innych cząstek elementarnych, to energia E pobierana przez taką cząstkę za pośrednictwem grawitonów przez nią absorbowanych, w czasie Δt, jest wprost proporcjonalna do pola powierzchni cząstki i czasu Δt.

E = E_sSΔt

E = E_s4πd²Δt

W ustalonych warunkach, w jednostce czasu, ilość energii absorbowanej przez cząstkę jest równa ilości energii przez nią emitowanej.

Założenie 3.

Masa grawitacyjna m* cząstki lub ciała, dla ustalonego obserwatora O, jest wprost proporcjonalna do masy grawitacyjnej m_g.

m* = ηm_g

Współczynnik η jest taki sam dla każdego obserwatora.

Jeżeli grawitony absorbowane przez materialną cząstkę o promieniu d, znajdującą się daleko od innych cząstek, pobierają z cząstek materii i przestrzeni energię E, w czasie Δt, to dla obserwatora, związanego z cząstką, wielkość

 

jest stała i nie zależy od rodzaju cząstki elementarnej.

Jeżeli w pewnej odległości od elementarnej cząstki znajdują się inne cząstki, to pewne elementy jej powierzchni mogą absorbować mniejsze ilości grawitonów, niż wówczas, gdy cząstka znajdowała się daleko od innych cząstek. Jeżeli zmniejszy się ilość grawitonów absorbowanych i emitowanych przez cząstkę, wówczas zmaleje ciśnienie wywierane przez grawitony na jej powierzchnię. Cząstka powiększy swoją powierzchnię, tak aby częściowo skompensować zmniejszenie swojej masy*. Jednak ilość energii E pobierana przez cząstkę, za pośrednictwem grawitonów przez nią absorbowanych, jest mniejsza od E_s4πd²Δt.

E < E_s4πd²Δt

Średni pęd przekazywany przez jeden grawiton do cząstki P jest równy

,

gdzie D_w jest odpowiednią odległością i wartością stałą.

Energia przekazywana przez jeden grawiton jest równa

.

Jeżeli E jest energią przekazywaną, w czasie Δt, do cząstki przez grawitony przez nią absorbowane, to ilość grawitonów absorbowanych przez elementarną cząstkę, w tym czasie, jest równa

Masa grawitacyjna m* cząstki, jest równa

Wartość liczbowa η jest równa ilości grawitonów oddziałujących z jednym kilogramem masy grawitacyjnej w czasie jednej sekundy.

Wartość liczbowa E_s jest równa ilości energii absorbowanej przez jednostkę powierzchni cząstki, znajdującej się daleko od innych cząstek, za pośrednictwem grawitonów, w jednostce czasu, dla obserwatora związanego z cząstką.

Pole powierzchni cząstki

S = 4Πd².

Masa grawitacyjna elementarnej cząstki, znajdującej się daleko od innych elementarnych cząstek, jest wprost proporcjonalna do pola jej powierzchni.

Masa bezwładna cząstki m_b (materii lub przestrzeni), poruszającej się z pewną prędkością względem obserwatora O, jest równa sumie masy grawitacyjnej m_g tej cząstki i masy równoważnej jej energii kinetycznej.

W zwykłych warunkach masa bezwładna jest niemal równa masie grawitacyjnej. W dalszym ciągu przyjmuję, że te masy są równe, gdy prędkość ciała jest niezbyt duża. Jeżeli cząstka pozostaje w spoczynku względem obserwatora O, to obie masy są równe.

W związku z nową definicją masy zmieniają się wymiary innych wielkości fizycznych, zależnych od masy. Wielkości fizyczne w nowym układzie jednostek MS* (metr, sekunda) są oznaczone symbolem *.

Pęd ciała

p^* = m^*v = ηmv            p^* = ηp.

Wymiarem pędu przy tak zdefiniowanej masie jest

.

Pęd p^* ma taki sam wymiar jak przyspieszenie.

F^* = m^*a = ηma            F^* = ηF            

W^* = F^*s = ηFs            W^* = ηW            

E^* = m^*c² = ηmc            E^* = ηE            

Oznaczmy przez masę bezwładną i zarazem grawitacyjną cząstki, spoczywającej w ustalonym układzie inercjalnym OXYZ, zmierzoną przez obserwatora O.

,

gdzie N jest ilością grawitonów oddziałujących z cząstką w czasie Δt. Jeżeli cząstka P porusza się ruchem jednostajnym, w układzie inercjalnym OXYZ, z prędkością v, to dla obserwatora O ta cząstka ma pewną energię kinetyczną, która powiększa masę bezwładną cząstki.

Masa bezwładna tej cząstki, zgodnie z STW, jest określona wzorem

.
 

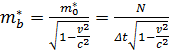Masa grawitacyjna cząstki nie zależy od ruchu cząstki względem danego obserwatora, ale może zależeć od własności tej części przestrzeni, w której znajduje się obserwator.

Niech masę* (grawitacyjną) cząstki wyznaczy obserwator O znajdujący się blisko tej cząstki. Jeżeli chcemy określić, jaką masę* ma cząstka dla obserwatora O' znajdującego się w innym miejscu niż O, to musimy uwzględnić masę* zmierzoną przez O oraz zależność między tempem upływu czasu dla tych obserwatorów.

Weźmy dwóch obserwatorów O i O' pozostających względem siebie w spoczynku. Obserwatorzy O i O' mogą inaczej ocenić masę* cząstki związanej z obserwatorem O. Zakładam, że obserwatorzy O i O' mają tak samo zbudowane zegary, które odmierzały takie samo tempo upływu czasu, gdy obserwatorzy byli w spoczynku względem siebie i blisko siebie. Później każdy z nich może być w innym miejscu. Obserwator O związany z cząstką wysyła w pewnej chwili sygnał radiowy. Następny sygnał wysyła po upływie czasu Δt, gdy stwierdzi, że z cząstką oddziałało N grawitonów od momentu wysłania poprzedniego sygnału itd. Obserwator O' odbiera te sygnały w odstępach czasu Δt', według wskazań własnego zegara. Masy* wyznaczone przez obserwatorów O i O' są odpowiednio i . Dla każdego z nich grawiton oddziałuje z cząstką albo nie, a więc N jest dla każdego jednakowe. Masy* ocenione przez obserwatorów O i O' zależą od tempa upływu czasu zegara związanego z tymi obserwatorami.

Masa* cząstki jest wprost proporcjonalna do ilości grawitonów oddziałujących z cząstką i odwrotnie proporcjonalna do tempa upływu czasu dla danego obserwatora. Jeżeli ilość grawitonów oddziałujących z cząstką zmienia się proporcjonalnie do tempa upływu czasu, to masa* cząstki pozostaje stała.

Wielkość masy* ciała zależy od obserwatora, który ją mierzy. Jednak każdy obserwator wyznaczający masę* tej samej cząstki, będącej w spoczynku względem niego i znajdującej się blisko niego, otrzyma taką samą wartość masy* cząstki. Masa* elektronu czy protonu zmierzona przez takiego obserwatora na Ziemi, Księżycu czy blisko Słońca jest liczbowo taka sama.

Założenie 4.

Dla obserwatora związanego z punktem materialnym masa* grawitacyjna i równocześnie masa bezwładna tego punktu materialnego jest stała, niezależnie od jego ruchu względem innych ciał i niezależnie od jego położenia względem innych ciał.

Tempo upływu czasu odmierzanego przez zegar związany z cząstką i masa* cząstki są ściśle ze sobą związane. Jeżeli z cząstką z jakiegokolwiek powodu oddziałuje mniej grawitonów, to proporcjonalnie zmniejsza się tykanie zegara i obserwator związany z cząstką otrzyma taką samą wartość liczbową masy*.

Weźmy dwie elementarne cząstki materii Q i P znajdujące się daleko od siebie i od innych cząstek elementarnych. Ich masy wyznaczone przez ustalonego obserwatora O są i .

Rys. 1.6.1.

Umieśćmy te cząstki blisko siebie w odległości mniejszej niż d_w. Każda z nich, według obserwatora O, absorbuje mniej grawitonów od strony drugiej cząstki niż z pozostałych kierunków, ponieważ część grawitonów, które mogłaby zabsorbować jedna z nich jest pochłonięta przez drugą. Z pozostałych kierunków cząstki absorbują nieco więcej grawitonów, ale całkowita ilość grawitonów oddziałujących z każdą z nich jest mniejsza niż wtedy, gdy znajdowały się daleko od siebie i innych cząstek. Równocześnie grawitony wirtualne emitowane przez cząstkę Q, w stronę cząstki P, nie są absorbowane przez cząstkę P.

Dla tego samego obserwatora O masy* tych cząstek, gdy znajdują się blisko siebie, są równe i ; są mniejsze niż ich masy*, gdy znajdowały się daleko od siebie i innych cząstek.

Masa ciała złożonego z n cząstek jest sumą mas* cząstek tworzących to ciało, jeżeli cząstki nie znajdują się zbyt blisko siebie. Oznaczmy przez masy* cząstek, przez N_i ilości grawitonów oddziałujących z tymi cząstkami w czasie Δt i przez N ilość grawitonów oddziałujących z tym ciałem.

Masa* cząstki zależy od jej położenia względem innych ciał materialnych. Jeżeli cząstka znajdzie się blisko innych cząstek, to jej masa* zmniejszy się, w porównaniu z masą*, którą by miała znajdując się daleko od innych cząstek. Jeżeli cząstki są gęsto upakowane, to z niektórymi cząstkami ciała może oddziaływać mniej grawitonów, niż gdyby były osobno w przestrzeni. Dla ustalonego obserwatora masa* układu cząstek, znajdujących się bardzo blisko siebie, jest mniejsza od masy* układu tych samych cząstek, gdy znajdują się w większych odległościach. Masa każdego ciała zależy od rozmieszczenia innych ciał we Wszechświecie.

Niech dla ustalonego obserwatora O ilości grawitonów oddziałujących w czasie Δt z cząstkami przestrzeni oraz materii, które znajdują się w elemencie objętości ΔV, są odpowiednio równe N_p i N_m. Wielkości oraz określone wzorami

i

będę nazywał odpowiednio gęstością* przestrzeni i gęstością* materii.

Jednostką gęstości* jest

.

Gęstość* przestrzeni lub materii jest równa ilości grawitonów oddziałujących z prze­strzenią lub materią znajdującą się w jednostce objętości, w jednostce czasu. Wielkości

i

są odpowiednio masą* przestrzeni i masą* materii, zawartej w elemencie objętości ΔV.

Niech z cząstką o masie oddziałuje średnio N₀ grawitonów w czasie Δt i średnia energia wewnętrzna cząstki jest równa N₀. Średnia masa* cząstki jest równa

.

Masa* cząstki jest wprost proporcjonalna do zawartej w niej energii.

.

Jeżeli zmaleje [wzrośnie] ilość grawitonów absorbowanych przez cząstkę, to ustala się nowa równowaga, przy czym ilość energii zawartej w cząstce zmaleje [wzrośnie], tak jak i jej masa*. Można zdefiniować masę cząstki, jako ilość energii zawartej w cząstce. Tak określona masa jest wprost proporcjonalna do masy*.

W dalszym ciągu pojęcia masy spoczynkowej cząstki i jej spoczynkowej energii wewnętrznej są równoważne. Całkowita energia cząstki jest równa sumie spoczynkowej energii wewnętrznej i energii kinetycznej tej cząstki. Energia potencjalna cząstki jest częścią energii wewnętrznej cząstki.