4.2. Kula oddziaływania grawitacyjnego
W skali całego Wszechświata na obiekty materialne i cząstki przestrzeni działają siły RW. Powoduje to oddalanie tych obiektów i cząstek przestrzeni od środka S Wszechświata, w różnych kierunkach i z różnymi prędkościami. Jednak takie obiekty jak Układ Słoneczny zachowują się niemal tak, jak gdyby znajdowały się w układzie inercjalnym. Możemy przyjąć, że Słońce znajduje się w środku kuli o promieniu R, stycznej do powierzchni Wszechświata, oraz że z ciałami Układu Słonecznego oddziałują, za pośrednictwem grawitonów, tylko cząstki materii i cząstki przestrzeni zawarte w tej kuli. Nazwijmy ją kulą oddziaływania grawitacyjnego. Wypadkowy pęd przekazywany do obiektów materialnych w naszej Galaktyce w wyniku ich oddziaływania z cząstkami materii i cząstkami przestrzeni znajdującymi się w kuli oddziaływania grawitacyjnego, jest wektorem zerowym. Kula oddziaływania grawitacyjnego jest bardzo duża i nasza Galaktyka, w porównaniu z nią, może być traktowana jak punkt materialny. Oddziaływanie między naszą Galaktyką i pozostałą częścią Wszechświata, za pośrednictwem grawitonów, zmienia równomiernie pęd materii w naszej Galaktyce, która w całości zachowuje się tak, jak swobodnie spadające ciało w polu grawitacyjnym. Układ odniesienia związany z naszą Galaktyką jest w przybliżeniu układem inercjalnym.
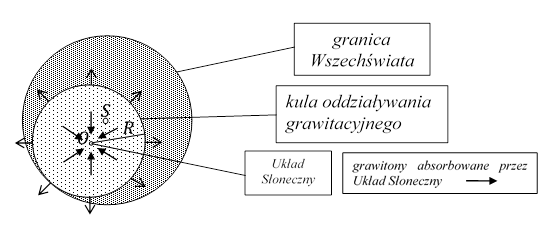
Rys. 4.2.1.
Dla każdego obiektu we Wszechświecie można określić taką kulę oddziaływania grawitacyjnego. Obiekty leżące dalej od środka S Wszechświata mają promień R odpowiednio mniejszy. W związku z tym, dla ustalonego obserwatora, masa ciał i siła grawitacji mogą być inne w różnych częściach Wszechświata.
Oszacujmy promień R takiej kuli oddziaływania grawitacyjnego, której środkiem O jest Słońce (Rys. 4.2.2.). W punkcie O umieśćmy punkt materialny P o masie 
. Obliczymy ilość grawitonów oddziałujących z tym punktem oraz cząstkami materii i przestrzeni tej kuli, w czasie Δt. Ilość grawitonów oddziałujących, w czasie Δt, z punktem materialnym P oraz z cząstkami materii i przestrzeni warstwy kulistej, o środku O i promieniach r i r + Δr , jest równa
,
gdzie 
jest średnią gęstością materii i przestrzeni dla kuli oddziaływania grawitacyjnego i
ΔV = 4πr2Δr.
Rys. 4.2.2.
Ilość wszystkich grawitonów oddziałujących z punktem materialnym P jest równa
.
Ponieważ
,
więc
.
Długość promienia R kuli oddziaływania grawitacyjnego jest bardzo duża w porównaniu z wartością dw, dlatego przyjmuję, że
.
Podstawiając
otrzymujemy
.
Promień kuli oddziaływania grawitacyjnego jest odwrotnie proporcjonalny do pierwiastka kwadratowego ze średniej gęstości materii i przestrzeni we Wszechświecie. Przyjmuję, że średnia gęstość materii i przestrzeni jest równa
.
Wówczas
.
W następnym podrozdziale 4.3. oszacowano wartość współczynnika η.
R = 1,33⋅1035 lat świetlnych
Promień R kuli oddziaływania grawitacyjnego zależy od średniej gęstości materii i przestrzeni oraz od współczynnika η. Obliczoną wartość R należy traktować szacunkowo, ponieważ średnia gęstość 
nie jest dokładnie znana i wartość η została tylko oszacowana.
Średnią gęstość materii i przestrzeni można wyrazić wzorem
.
Przestrzeń zawarta w kuli oddziaływania grawitacyjnego rozszerza się podobnie jak w całym Wszechświecie. Przyspieszenie obszaru przestrzeni odległego o r od Układu Słonecznego (punkt O) jest równe
.
Dla odległości r = 10 miliardów lat świetlnych 
.
W ciągu jednego miliona lat prędkość oddalania wzrośnie o 
.
Kula oddziaływania grawitacyjnego, jak cały Wszechświat, rozszerza się równomiernie we wszystkich kierunkach, względem Ziemi, zachowując swój kulisty kształt.