4.3. Oddziaływanie grawitonów z materialną kulą

Jeżeli grawitony oddziałują z punktem materialnym, o masie m, tylko z jednej strony, wówczas siła działająca na niego jest największa. Obliczmy wartość liczbową takiej siły.

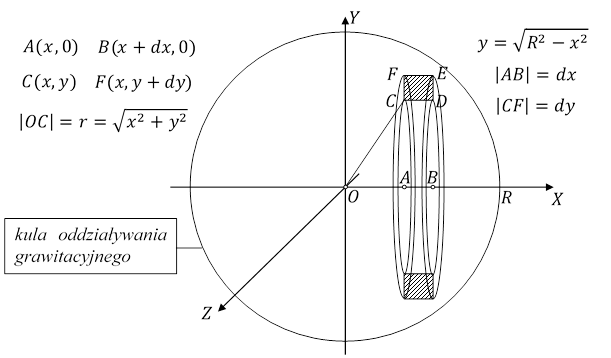
Rys. 4.3.1.

Ilość grawitonów oddziałujących z punktem materialnym o masie m, znajdującym się w początku układu współrzędnych O, oraz materią i przestrzenią zawartą w pierścieniu, jest równa

Grawiton oddziałujący między punktem materialnym P i cząstką przestrzeni lub materii znajdującą się w punkcie C(x,y,z), przekaże do punktu materialnego pęd określony wzorem

Pęd przekazany do punktu materialnego przez materię i przestrzeń zawartą w pierścieniu jest równy

Wartość liczbowa całkowitego pędu przekazanego przez grawitony oddziałujące z punktem materialnym oraz cząstkami materii i przestrzeni znajdującymi się w półprzestrzeni ograniczonej płaszczyzną OYZ, w której znajduje się dodatnia półoś OX, jest równa

Siła, z jaką oddziałują z punktem materialnym cząstki materii i przestrzeni, znajdujące się z jednej jego strony, jest równa

gdzie R jest promieniem kuli oddziaływania grawitacyjnego.

Jest to największa wartość siły oddziaływania grawitacyjnego, jaka może działać na ciało o masie m.

W dalszym ciągu przyjmuję, że

Przyjętą wartość η należy traktować szacunkowo. Przypuszczam, że wprowadzona wartość η jest bliska rzeczywistej.

F₁ = 2,6⋅10¹³m N

Weźmy punkt materialny o masie m na powierzchni kuli, która zachowuje się tak, jak cząstka elementarna, to znaczy oddziałuje z grawitonami tylko na swojej powierzchni. Na ten punkt materialny działa siła

. (patrz 3.2.)

F_max = F₁.

Jeżeli

to promień kuli oddziaływania grawitacyjnego, dla Układu Słonecznego, jest równy

R = 1,33⋅10³⁵ lat świetlnych

Dla elementarnej cząstki materii o masie m i promieniu d jest prawdziwy wzór

(patrz 1.7.).

Ponieważ

więc

Dla elektronu

Promień elektronu

d_e = 1,5⋅10^-27 m

i jest znacznie większy od

Weźmy materialną kulę K o masie m, środku w punkcie S i promieniu d znajdującą się daleko od innych ciał materialnych. Kula może być również cząstką elementarną, na przykład elektronem. Obliczmy ilość grawitonów Δn oddziałujących z kulą, w czasie Δt, które są emitowane oraz absorbowane przez kulistą warstwę materii i przestrzeni, ograniczoną sferami o środku w punkcie S i promieniach r i r + Δr . Czas, odległość i masa są mierzone przez ustalonego obserwatora O.

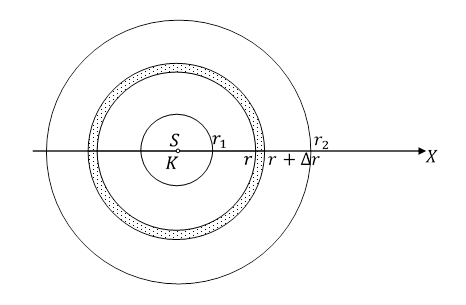
Rys. 4.3.2.

ΔV_warstwy - 4πr²Δr

Ilość grawitonów oddziałujących z kulą K i warstwą kulistą jest wprost proporcjonalna do odległości środka kuli od tej warstwy. W jednostce czasu z kulą oddziałuje

grawitonów.

Ilość grawitonów oddziałujących, w jednostce czasu, z kulą i warstwą kulistą o środku S i promieniach r₁ i r₂ (r₁ < r₂) jest równa

Masa elektronu

m_e = 9,11⋅10^-31 kg .

Z elektronem oraz materią i przestrzenią, w czasie jednej sekundy, oddziałuje około 9,11⋅10⁶⁷ grawitonów. Dla elektronu

Ilość grawitonów oddziałujących, w jednostce czasu, z elektronem oraz przestrzenią i materią zawartą w kuli o promieniu r, której środkiem jest elektron, jest równa

r[m]	10²⁵	10³⁰	10³⁵	10⁴⁰	10⁴⁵	10⁵⁰
	6⋅10¹⁵	6⋅10²⁵	6⋅10³⁵	6⋅10⁴⁵	6⋅10⁵⁵	6⋅10⁶⁵

Obliczymy ciśnienie działające na powierzchnię kuli K, o masie m i promieniu d, wywierane przez grawitony oddziałujące z nią oraz przestrzenią i materią zawartą w warstwie kulistej, w czasie Δt.

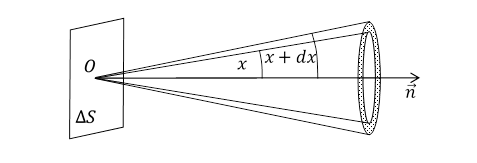
Rys. 4.3.3.

Z elementem ΔS powierzchni kuli oddziałuje

grawitonów. Te grawitony poruszają się pod różnymi kątami w stosunku do powierzchni ΔS, przy czym równomiernie z każdego kierunku.

Kąty bryłowe o wierzchołku w punkcie O odpowiadające kątowi x i x + x mają miary

Miara kąta bryłowego o mierze , z którego wycięto kąt bryłowy o mierze jest równa

Z kąta bryłowego o mierze , w czasie Δt, z elementem ΔS oddziałuje

grawitonów. Każdy grawiton przekazuje pęd

a jego składowa prostopadła do elementu powierzchni jest równa

Do elementu powierzchni ΔS z kąta o mierze , w czasie Δt, jest przekazywany pęd

Pęd przekazany przez wszystkie grawitony oddziałujące z tym elementem oraz przestrzenią i materią warstwy kulistej jest równy

Pęd przekazywany do ΔS przez grawitony oddziałujące z tym elementem oraz materią i przestrzenią zawartą w kuli oddziaływania grawitacyjnego jest równy

Na element ΔS działa siła

Ciśnienie wywierane na powierzchnię kuli przez grawitony określa wzór

Jeżeli kula o masie m i promieniu d jest podobna do cząstki elementarnej, to jej masa może być określona wzorem

Ciśnienie wywierane na jej powierzchnię przez grawitony jest równe

Dla każdej takiej kuli ciśnienie nie zależy od masy kuli i jej wielkości. Jest to największe możliwe ciśnienie, jakie grawitony mogą wywierać na powierzchnię takiej kuli.

Jest to bardzo duże ciśnienie, ale nie jest nieskończone. Nawet dla bardzo dużej masy kuli ciśnienie ma skończoną wartość, .

Ciśnienie wywierane na powierzchnię elektronu przez grawitony chroni go przed rozpadem, jeżeli oddziaływania między elementami jego ładunku elektrycznego są odpowiednio mniejsze niż w prawie Coulomba.

Każda cząstka elementarna ma pewien średni poziom energii wewnętrznej, określony przez ilość grawitonów przez nią absorbowanych. Jeżeli cząstka elementarna ma energię wewnętrzną powyżej średniej, to ciśnienie wywierane przez grawitony na cząstkę jest za małe i cząstka emituje nadmiar swojej energii wewnętrznej przy pomocy grawitonów. Gdy energia wewnętrzna jest poniżej średniej wówczas cząstka emituje mniej grawitonów niż absorbuje i powiększa swoją energię.

Cząstki nieustannie absorbują grawitony powiększając swoją energię wewnętrzną, wobec tego muszą emitować grawitony dla jej zmniejszenia. W ten sposób funkcjonuje mechanizm stałej wymiany energii i pędu między elementarnymi cząstkami materii i przestrzeni.

Stabilne istnienie cząstek elementarnych materii jest możliwe dzięki ciśnieniu wywieranemu na nie przez grawitony. W przypadku braku tego ciśnienia cząstki uległy by destrukcji. Cząstka jest trwała, jeżeli występuje równowaga między ciśnieniem wewnętrznym, zależnym od jej energii wewnętrznej, oraz ciśnieniem zewnętrznym wywieranym przez grawitony. Jeżeli powstanie cząstka, w której ciśnienie wewnętrzne jest znacznie większe, niż ciśnienie wywierane przez grawitony, wówczas może ulec rozpadowi na inne zrównoważone cząstki i pozbywa się nadmiaru energii. Być może, dlatego mezony są cząstkami nietrwałymi.

Przyjmuje się, że siła grawitacji ma znaczenie w skali kosmosu, natomiast pomija się jej znaczenie dla cząstek elementarnych. Jest to błędny pogląd. Siła grawitacji jest ogromna zarówno w świecie gwiazd i galaktyk jak i w skali cząstek elementarnych. Gdyby nie było ciśnienia wywieranego na cząstki elementarne przez grawitony, to materia nie istniałaby w znanej nam postaci. Dzięki oddziaływaniu grawitacyjnemu istnieją gwiazdy i cząstki elementarne.

Czy woda w doświadczeniu Newtona z wiadrem podnosi się do góry przy brzegu wiadra, gdy wiadro wiruje również względem absolutnej, pustej przestrzeni? Jeżeli we Wszechświecie byłoby tylko wiadro z wodą, wówczas cząstki elementarne materii wody i wiadra uległy by rozpadowi ze względu na brak ciśnienia wywieranego przez grawitony na te cząstki. Wiadro i woda w takim świecie nie mogłoby istnieć, zatem pytanie, czy woda reaguje na obrót w pustej przestrzeni jest pozbawione sensu. Jeżeli w OTW wynika, że takie oddziaływanie jest możliwe, to jakieś jej założenie jest błędne. Błędne jest milczące założenie, że mogą istnieć cząstki materii w pustej przestrzeni.

Być może podczas grawitacyjnego zapodania się gwiazdy o bardzo dużej masie jej gęstość stanie się tak duża, że cząstki elementarne wewnątrz gwiazdy przestaną oddziaływać z zewnętrznymi cząstkami materii i przestrzeni. Powstanie gwiazda złożona tylko z kwarków, dla której zewnętrzne ciśnienie grawitacyjne jest równoważone przez ciśnienie degeneracji kwarków.

Prędkość światła blisko powierzchni takiej kuli o promieniu

dla dalekiego obserwatora O' jest równa

Fotony mogą opuszczać taką gwiazdę. W miarę oddalania od takiej gwiazdy ich energia maleje.

Materialna cząstka emituje grawitony równomiernie we wszystkich kierunkach przestrzeni. Jeżeli czynnik zewnętrzny spowoduje asymetrię tej emisji, wówczas na cząstkę działaby siła wynikająca z przekazywania jej niezerowego pędu przez emitowane grawitony. Przypuśćmy, że materialna płyta emituje więcej grawitonów z jednej swojej strony niż z drugiej.

Rys. 4. 3.4.

Otrzymalibyśmy w ten sposób silnik odrzutowy, którego działanie wymagałoby jedynie dostarczania energii dla podtrzymania takiej emisji.

Innym rodzajem takiego silnika byłaby płyta, która w większym stopniu absorbowała by grawitony dochodzące do niej z jednej strony niż z drugiej.

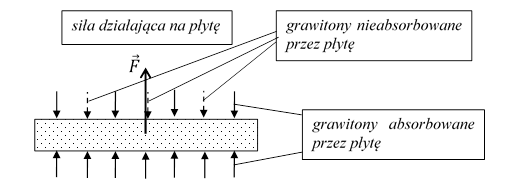
Rys. 4. 3.5.

Jaki czynnik może spowodować taką asymetryczną emisję lub absorpcję grawitonów?

Być może pole elektryczne powoduje taką asymetrię emisji lub absorpcji grawitonów i stąd efekt Biefelda-Browna.