1.1. Szybkość rozchodzenia się oddziaływania grawitacyjnego. Czy zasada względności jest prawdziwa?

Przypuśćmy, że oddziaływanie grawitacyjne dwóch materialnych ciał jest ich wzajemnym przyciąganiem i to oddziaływanie jest przekazywane z jednego ciała do drugiego z prędkością światła c. Weźmy dwie jednakowe kule o masie m każda, połączone sztywnym prętem w ten sposób, że odległość środków tych kul jest równa d. Takie dwie kule połączone sztywnym prętem nazywam obiektem 2k.

Załóżmy, że istnieje układ inercjalny UI, w którym na te spoczywające kule nie działają żadne siły, niezależnie od ich ustawienia w przestrzeni. Niech te kule poruszają się ruchem jednostajnym z prędkością w układzie inercjalnym UI tak, że pręt łączący kule tworzy kąt o mierze γ z wektorem prędkości. Ze względu na skończoną szybkość rozchodzenia się oddziaływania grawitacyjnego, kula znajdująca się w punkcie A oddziałuje z kulą znajdującą się w punkcie B' natomiast kula znajdująca się w punkcie B oddziałuje z kulą znajdującą się w punkcie A'.

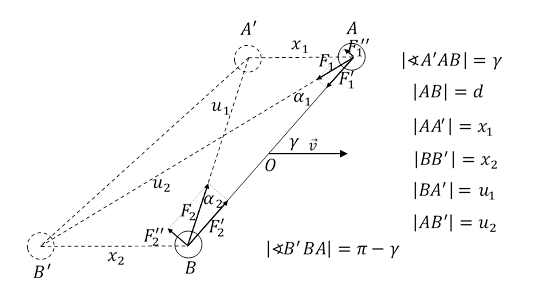
Rys. 1.1.1.

Oznaczmy przez t₁ czas potrzebny na przebycie odległości u₁ między kulami B i A' przez światło w danym układzie inercjalnym.

u₁ = ct₁.

W tym czasie kula A przesunie się z punktu A' do punktu A o odcinek

x₁ = vt₁.

Stąd otrzymujemy

Na kulę znajdującą się w punkcie B działa siła przyciągania

(mająca zwrot wektora ) pochodząca od kuli A tak, jakby ta ostatnia znajdowała się w punkcie A' (ze względu na skończoną szybkość rozchodzenia się oddziaływania grawitacyjnego). Wartość siły F₂ może być inna, ale dla oszacowania przyjąłem wzór Newtona. Składowa tej siły równoległa do pręta ma wartość

natomiast składowa prostopadła do pręta

Oznaczmy przez t₂ czas potrzebny na przebycie odległości u₂ między kulami A i B' przez światło w danym układzie inercjalnym.

u₂ = ct₂.

W tym czasie kula B przesunie się z punktu B' do punktu B o odcinek

x₂ = vt₂.

Stąd otrzymujemy

α₂ = α₁

Na kulę znajdującą się w punkcie A działa siła przyciągania F₁ (mająca zwrot wektora )

pochodząca od kuli B tak jakby ta ostatnia znajdowała się w punkcie B'.

Składowa tej siły równoległa do pręta ma wartość

natomiast składowa prostopadła do pręta

Na obiekt 2k, względem środka pręta, działa moment siły określony wzorem

Dla i moment siły jest różny od zera i stara się ustawić obiekt 2k równolegle do kierunku ruchu.

Równolegle do pręta działa wypadkowa siła

o zwrocie od punktu B do punktu A.

Prostopadle do pręta działa siła

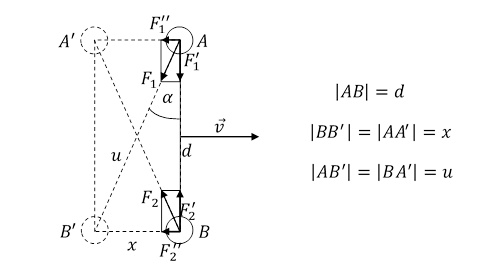
Rys. 1.1.2.

W przypadku moment siły M₀ = 0, F_r = 0 i obiekt 2k porusza się bez zmiany swojego ustawienia względem wektora prędkości. To ustawienie nie jest stabilne. Wystarczy niewielka zmiana tego ustawienia i na ten obiekt działa moment siły starający się ustawić go równolegle do wektora prędkości.

Na obiekt 2k działa siła

przeciwnie do zwrotu wektora prędkości, która hamuje ruch tego obiektu.

Układ złożony z tych kul jest więc hamowany, siłą F_p, ze względu na ich wzajemne oddziaływanie grawitacyjne. Hamowanie to wystąpi, gdy tylko siła F₁ > 0. W tych obliczeniach nie uwzględniałem oddziaływania grawitacyjnego między cząstkami dla każdej z tych kul z osobna. Efektu hamowania dla układu obu kul nie byłoby wtedy, gdyby na pojedynczą kulę działała siła przeciwna do siły F₁ pochodząca z wzajemnego oddziaływania grawitacyjnego cząstek tej kuli. Wtedy jednak jedna kula poruszająca się z prędkością v w układzie inercjalnym byłaby przyspieszana tylko ze względu na wzajemne oddziaływanie grawitacyjne swoich cząsteczek.

Siły te są bardzo małe w zwykłych warunkach, ale z przyjętych założeń wynika, że istnieją.

Jeżeli każda kula ma masę 100 kg, odległość między nimi jest 2 m i kule poruszają się z prędkością , to siła działająca na nie jest w przybliżeniu równa 10^-11 N. Przyspieszenie działające na te kule jest .

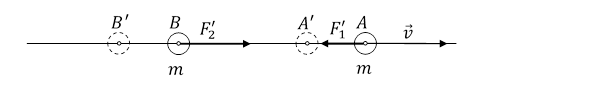
Rys.1.1.3.

W przypadku γ = 0 moment siły M₀ = 0, F_p = 0 i obiekt 2k porusza się bez zmiany swojego ustawienia względem wektora prędkości. To ustawienie jest stabilne. Jeżeli zmienimy to ustawienie to na obiekt działa moment siły starający się przywrócić poprzednie ustawienie.

Siła wypadkowa działająca na układ kul jest równa

Siła F_r ma zwrot zgodny ze zwrotem wektora prędkości i powoduje wzrost prędkości układu złożonego z kuli A i kuli B.

gdzie

Jeżeli uwzględnimy skracanie długości w kierunku ruchu to zamiast długości d należy podstawić

Weźmy dwie jednakowe kule, o masie m każda, połączone sztywnym prętem o długości 2r. Kule poruszają się po okręgu o promieniu r dookoła środka pręta O z prędkością liniową v, w układzie inercjalnym UI.

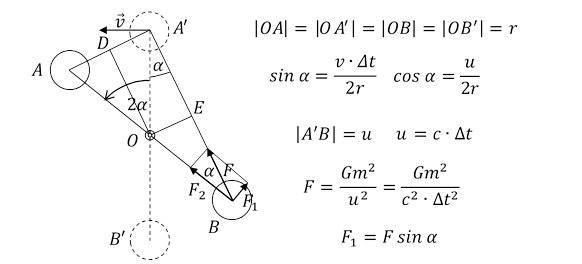
Rys. 1.1.4.

W czasie Δt, gdy światło przebędzie odległość |A'B|, pręt obróci się o kąt 2α.

Na kulę B działa siła

prostopadła do pręta AB.

Na kulę A działa siła równa, co do wartości F₁, ale przeciwnie skierowana. Układ dwu kul obracający się dookoła środka ciężkości z prędkością kątową różną od zera, zwiększa swoją prędkość ze względu na wzajemne oddziaływanie grawitacyjne swoich cząstek.

Jeżeli każda kula ma masę 100 kg i porusza się z prędkością po okręgu o promieniu 10 m (gdyby to było możliwe), to siła F₁ działająca na każdą z nich jest w przybliżeniu równa 10 ^-14 N. Przyspieszenie jest .

Dwie gwiazdy o zbliżonej masie obiegające wspólny środek masy powinny poruszać się z coraz większą prędkością kątową, czego w rzeczywistości się nie obserwuje ze względu na znikome wartości działających sił w porównaniu z innymi siłami, które na te gwiazdy działają.

Dla ciała materialnego w kształcie kuli efekt przyspieszania lub hamowania jest znikomy lub zerowy.

Pokazane wyżej efekty są wynikiem początkowego założenia: oddziaływanie grawitacyjne dwóch materialnych ciał jest ich wzajemnym przyciąganiem i to oddziaływanie jest przekazywane z jednego ciała do drugiego z prędkością światła c. Pokazane wyżej efekty wystąpią również dla dowolnej skończonej prędkości rozchodzenia się oddziaływania grawitacyjnego.

Na obiekt 2k działa siła hamująca lub przyspieszająca, w zależności od jego ustawienia w stosunku do wektora prędkości, gdy te kule poruszają się z prędkością v w układzie inercjalnym UI. Siły te są jedynie wynikiem wzajemnego oddziaływania grawitacyjnego kul obiektu 2k. Stanowi to sprzeczność z zasadą zachowania pędu.

Wielkość tej siły zależy od prędkości kul w układzie inercjalnym UI. Można wybrać takie układy inercjalne, w których ta siła nie istnieje, jeśli kule są w spoczynku lub takie, w których ta siła jest bardzo duża. Stanowi to sprzeczność z zasadą względności.

Początkowo sądziłem, że opisane efekty są niemożliwe ze względu na zasady zachowania energii i pędu. Potem jednak zrozumiałem, że te efekty mogą występować w rzeczywistości i nie naruszają zasad zachowania pędu i energii. Można je wyjaśnić w przedstawionej dalej teorii, w której oddziaływanie grawitacyjne polega na wymianie energii i pędu między cząstkami materii oraz cząstkami przestrzeni za pośrednictwem grawitonów, poruszających się z prędkością światła. Opisane efekty są przykładami wymiany pędu i energii między ciałami materialnymi oraz cząstkami przestrzeni i cząstkami materii Wszechświata. Układy ciał materialnych nigdy nie są izolowane od pozostałych cząstek Wszechświata. Zasady zachowania pędu i energii należy uogólnić tak, aby uwzględniały oddziaływanie materialnych ciał również z pozostałymi cząstkami materii i cząstkami przestrzeni. W dalszym ciągu zakładam, że prędkości kul są małe w stosunku do prędkości światła.

Jeżeli oddziaływanie grawitacyjne rozchodzi się ze skończoną prędkością, to nie mogą istnieć dwa układy inercjalne poruszające się względem siebie z prędkością , w których na unieruchomiony w tych układach, dowolnie zorientowany obiekt 2k nie działają żadne siły.

Jeżeli istnieje wyróżniony inercjalny układ UI, w którym na unieruchomiony, dowolnie zorientowany obiekt 2k nie działają żadne siły, to w układzie U₁ poruszającym się z prędkością

względem UI, na unieruchomiony obiekt 2k ustawiony równolegle do wektora działa siła

gdzie

Jeżeli inercjalny układ U₂ porusza się z prędkością względem U₁, a więc z prędkością względem UI, to na unieruchomiony obiekt 2k ustawiony równolegle do wektora działa siła

Taki wyróżniony układ UI istnieje. Jeżeli obserwator O związany z układem inercjalnym U₁ stwierdzi, że na unieruchomiony, dowolnie zorientowany obiekt 2k nie działa żadna siła, to znaczy, że U₁ jest układem UI. W przeciwnym przypadku obserwator ustawia obiekt 2k tak, aby M₀ = 0 i F_p = 0.

Jeżeli na obiekt 2k przy takim ustawieniu działa siła o wartości , to obserwator O porusza się względem układu UI z prędkością

i wyróżnionym układem UI jest taki, który porusza się względem niego z prędkością

Wektor jest równoległy do pręta łączącego kule. Dla każdego układu inercjalnego U₁ wyróżniony układ UI jest taki sam z dokładnością do przesunięcia i obrotu.

Obserwator O znajdujący się w zamkniętym pomieszczeni może stwierdzić, z jaką prędkością porusza się względem wyróżnionego układu UI bez wyglądania na zewnątrz. Wyróżniony układ UI jest układem lokalnym.

Jeżeli oddziaływanie grawitacyjne rozchodzi się z prędkością światła, to zasada względności nie jest prawdziwa. Można ją jednak stosować z bardzo dobrym przybliżeniem.

Jeżeli przyjmiemy, że zasada względności jest prawdziwa, to prędkość rozchodzenia się oddziaływania grawitacyjnego jest nieskończona. Wówczas trzeba przyjąć, że istnieje pewien wyróżniony układ odniesienia, w którym oddziaływanie grawitacyjne rozchodzi się z nieskończoną prędkością. Niezależnie od tego czy prędkość rozchodzenia się oddziaływania grawitacyjnego jest skończona czy nieskończona musimy przyjąć istnienie wyróżnionego układu odniesienia, w którym grawitacja ma szczególny charakter.

Założenie, że oddziaływanie grawitacyjne rozchodzi się z nieskończoną prędkością wydaje się trudne do przyjęcia.

W dalszym ciągu przyjmuję, że grawitony poruszają się z prędkością światła.

Z tego założenia wynika, że oddziaływanie grawitacyjne rozchodzi się z prędkością światła.