5.5. Oddziaływanie wirującej materialnej kuli z elementem materii lub przestrzeni

Kula K o masie M porusza się po okręgu o środku S i promieniu d z prędkością kątową ω. W odległości r od punktu S w punkcie P znajduje się punkt materialny o masie m.

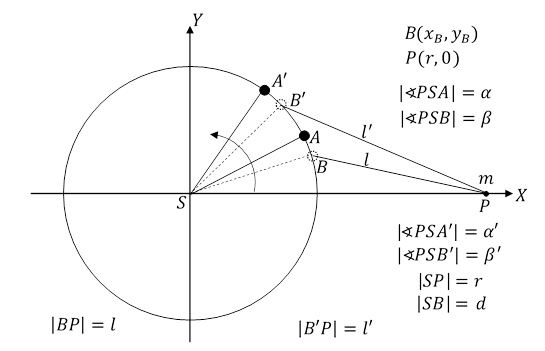
Rys. 5.5.1.

Jeżeli kula znajduje się punkcie A, to oddziałuje z punktem materialnym tak, jak gdyby znajdowała się w punkcie B, ze względu na skończoną prędkość grawitonów. Kula przejdzie z punktu B do A w czasie

potrzebnym grawitonom na przebycie odległości od B do P. W tym czasie promień wodzący kuli obróci się o kąt, którego miara jest równa

.

Kąt

.

Odpowiednio dla A' kąt

.

Jeżeli kąt β wzrośnie o

Δβ = β' - β,

to odpowiednio kąt α wzrośnie o

w czasie

.

Podczas przejścia kuli z B do B' do punktu materialnego przekazywany jest pęd

.
 

l² = d² + r² - 2dr cos β
 

l'² = d² + r² - 2dr cos(β + Δβ)
 

y_B = d sin β

Składowa wektora równoległa do osi SY jest równa

.

Podczas jednego obiegu okręgu przez kulę do punktu materialnego, ze względu na obecność kuli, zostanie przekazany pewien pęd a jego składowa równoległa do osi SY jest równa

.
 

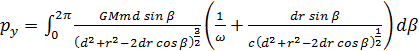
Podstawmy nową zmienną

u = β = π.
 

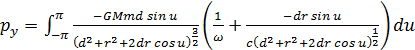
Oznaczmy

a = d² + r²

i

b = 2dr .
 

Pierwsza całka jest równa zero, ponieważ funkcja podcałkowa jest nieparzysta.

Stosując całkowanie przez części otrzymujemy.

Podczas jednego obiegu kuli po okręgu składowa pędu równoległa do osi SY przekazana do punktu materialnego jest równa

.

Jeden obieg jest wykonywany w czasie .

Średnia siła działająca na punkt materialny równolegle do osi SY jest równa

.

Istnienie tej siły jest skutkiem skończonej prędkości rozchodzenia się oddziaływania grawitacyjnego, za pośrednictwem grawitonów. Z tego powodu czas t_o oddalania się punktu B od punktu materialnego jest dłuższy niż czas t_z jego zbliżania. Miara kąta α rośnie proporcjonalnie do czasu, natomiast miara kąta β nie, ze względu na okresową zmianę odległości punktu B od punktu P. Podczas oddalania do punktu materialnego przekazywany jest pęd p_y+ o zwrocie zgodnym ze zwrotem osi SY, podczas zbliżania pęd p_y- o zwrocie przeciwnym. Ponieważ

t_o > t_z,

więc

p_y+ > p_y-

i

p_y = p_y+ - p_y- > 0 .

Kula K o masie M porusza się po okręgu o środku S₁(0,0,z) i promieniu d, w płaszczyźnie prostopadłej do osi SZ, z prędkością kątową ω. W odległości r od początku prostokątnego układu współrzędnych S, na osi SX, w punkcie P(r,0,0) znajduje się punkt materialny o masie m.

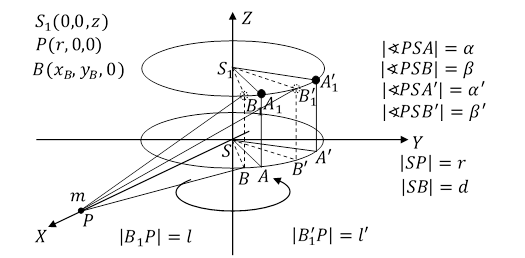
Rys. 5.5.2.
 

l² = z² + d² + r² - 2dr cos β
 

l'² = z² + d² + r² - 2dr cos(β + Δβ)
 

Podczas przejścia kuli z B₁ do do punktu materialnego przekazywany jest pęd

,

a jego składowa równoległa do osi SY jest równa

.

Podczas jednego obiegu okręgu przez kulę do punktu materialnego zostanie przekazana składowa

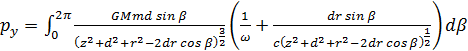
Podstawmy nową zmienną

u = β = π.
 

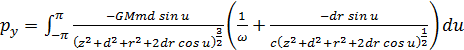
Oznaczmy

a = z² + d² + r²

i

b = 2dr .
 

Średnia siła działająca na punkt materialny równolegle do osi SY jest równa

.

Zamiast kuli weźmy cienki pierścień o masie M, promieniu d, obracający się z prędkością ω w płaszczyźnie prostopadłej do osi SZ dookoła punktu S₁.

Składowa F_y siły działającej na punkt materialny w wyniku obrotu pierścienia jest określona takim samym wzorem jak w przypadku kuli, ale w tym przypadku pozostaje taka sama w każdej chwili.

Weźmy jednorodną materialną kulę o środku w punkcie S, promieniu R, masie M i gęstości , obracającą się z prędkością kątową ω dookoła osi SZ w zwrocie od dodatniej części osi SX do dodatniej części osi SY. Na zewnątrz kuli, w punkcie P na osi SX znajduje się punkt materialny o masie m. Wszystkie te wartości są mierzone przez obserwatora O znajdującego się blisko punktu P. Dla uproszczenia zapisu układ współrzędnych obserwatora O został przesunięty tak, że pokrywa się z układem SXYZ. W kuli wycinam pierścień o osi SZ, ograniczony płaszczyznami prostopadłymi do osi SZ i przechodzącymi przez punkty o współrzędnych (0,0,z) i (0,0,z + Δz), o promieniach x i x + Δx, szerokości Δx i grubości Δz. Objętość tego pierścienia

ΔV = 2πxΔxΔZ

a jego masa

.

Pierścień wiruje z prędkością kątową ω.

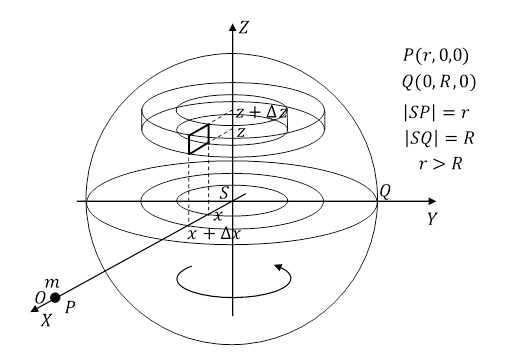
Rys. 5.5.3.

Pierścień działa na punkt materialny pewną siłą, której składowa równoległa do osi SY jest równa

.

Składowa siły z jaką kula oddziałuje na punkt materialny, równoległa do osi SY jest równa

.
 

Podstawiając nową zmienną

u = x² + z² - r² ,
 

,

otrzymujemy

.
 

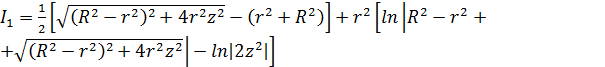
Ponieważ funkcja podcałkowa jest parzysta, więc

.
 

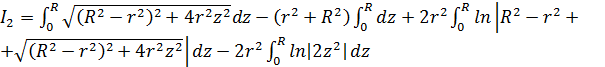
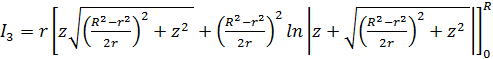
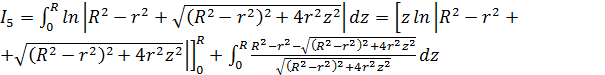
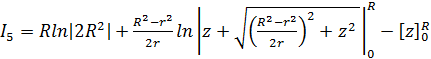
Dla

r < R

mamy

.

Po podstawieniu i wykonaniu odpowiednich działań otrzymujemy.

Na element materii lub przestrzeni o masie m, znajdujący się w punkcie P działa siła

,

prostopadła do wektora w płaszczyźnie równikowej kuli.

Siła ta powoduje, że swobodne cząstki przestrzeni znajdujące się blisko kuli poruszają się dookoła kuli zgodnie z jej obrotem. W ten sposób moment pędu kuli jest przenoszony do przestrzeni i kula stopniowo zmniejsza swoją prędkość kątową, w stosunku do cząstek przestrzeni. Przestrzeń dookoła kuli zyskuje pewien moment pędu, który poprzez wzajemne oddziaływanie cząstek przestrzeni rozprasza się w całej przestrzeni. Po bardzo długim czasie kula będzie nieruchoma w stosunku do cząstek przestrzeni, jeżeli w tym czasie nie oddziałuje z cząstkami materii. Pochłanianie materii przez kulę może zmienić jej pęd.

Cząstki przestrzeni oraz cząstki materii znajdujące się blisko takiej kuli zyskują dodatkowy moment pędu zgodny z momentem pędu kuli. Największy moment pędu jest przekazywany do tych cząstek, które są najbliżej kuli.

Dla Ziemi siła

,

działająca na ciało o masie 1 kg, znajdujące się w odległości dwóch promieni Ziemi od jej środka, jest równa

F_y = 3,8⋅10^-7 N .

Odpowiednio przyspieszenie uzyskane przez to ciało jest

.

Gdyby Słońce miało promień R = 100 km, to w odległości 2R od jego środka siła działająca na 1 kg masy byłaby równa

F_y = 1,1⋅10⁵ω N .

Dla

,

co odpowiada prędkości liniowej w odległości R od osi obrotu

,

siła działająca na 1 kg masy jest równa

F_y = 1,1⋅10⁶ N ,

a przyspieszenie tego elementu

.

Takie siły działają na masę m, pozostającą w spoczynku, w układzie współrzędnych w którym wiruje kula. Po pewnym czasie cząstki materii lub przestrzeni zaczynają obiegać kulę, zmniejszając swoją prędkość względem jej powierzchni i wówczas wartość siły i przyspieszenia maleje.

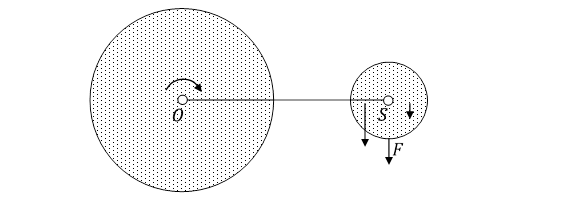
Rys. 5.5.4.

Jeżeli w pobliżu wirującej kuli umieścimy drugą, początkowo nieruchomą, to działa na nią siła F, prostopadła do odcinka OS, która powoduje obieganie pierwszej kuli przez drugą (o ile to jest możliwe) w kierunku zgodnym z obrotem pierwszej kuli. Ponadto druga kula zacznie wirować w przeciwną stronę niż pierwsza. Te efekty powinny być widoczne dla bardzo masywnej kuli wirującej z dostatecznie dużą prędkością.

Jeżeli dwa masywne ciała obiegają się nawzajem, to ich moment pędu zmniejsza się wskutek ich oddziaływania z cząstkami przestrzeni. Powoduje to, że zbliżają się do siebie poruszając się po coraz ciaśniejszych orbitach.