4.1. Oddziaływanie grawitacyjne w skali Wszechświata

W skali gromady galaktyk oddziaływanie grawitacyjne, między cząstkami materii oraz cząstkami przestrzeni i cząstkami pozostałej materii, powoduje powstawanie sił działających na ciała materialne, tak jak gdyby te ciała nawzajem się “przyciągały”. Inaczej wygląda to w skali całego Wszechświata.

Przestrzeń, tak jak i materia, ma pewną bezwładność. Stąd wynika, że dla dowolnego ustalonego obserwatora, żadna część przestrzeni nie może poruszać się z prędkością większą od prędkości światła. Grawiton, jak również foton, poruszający się z prędkością światła, może przebyć odległość między dowolnymi punktami Wszechświata w skończonym czasie, pomimo jego rozszerzania. Każda elementarna cząstka jest otoczona chmurą, nieustannie emitowanych, wirtualnych grawitonów rozciągającą się na cały Wszechświat. Z cząstkami Ziemi mogą oddziaływać grawitony emitowane przez cząstki znajdujące się nawet na krańcach Wszechświata.

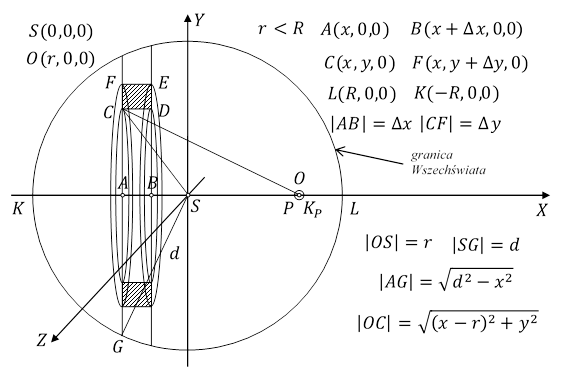
Rys. 4.1.1.

Zakładam, że Wszechświat jest kulą o środku S i promieniu R, utworzoną z cząstek przestrzeni, w której znajdują się cząstki materii, przy czym w dużej skali cząstki przestrzeni oraz cząstki materii są równomiernie rozłożone we Wszechświecie. Cząstki przestrzeni tworzą gaz, dla którego w każdym miejscu jest określona gęstość i odpowiednie ciśnienie wytworzone przez wzajemne oddziaływanie tych cząstek. Materia nie oddziałuje bezpośrednio z cząstkami przestrzeni, lecz jedynie za pośrednictwem grawitonów.

Weźmy punkt materialny P, o masie , znajdujący się w odległości r od środka S. K_P jest kulą o środku P i promieniu d_w.

Oznaczmy średnią gęstość materii i średnią gęstość przestrzeni, dla całego Wszechświata, odpowiednio przez i . Łączna średnia gęstość przestrzeni i materii

.

Wyznaczmy siłę działającą na punkt materialny P w wyniku jego oddziaływania z cząstkami materii i przestrzeni Wszechświata.

Ilość grawitonów oddziałujących między punktem materialnym P oraz cząstkami materii i przestrzeni pierścienia powstałego przez obrót prostokąta CDEF dookoła osi OX, jest równa

.

jest średnią gęstością materii i przestrzeni dla całego Wszechświata i

ΔV = 2πyΔxΔy

jest objętością pierścienia.

Grawiton zaabsorbowany lub wyemitowany przez punkt materialny P, który został odpowiednio wyemitowany lub zaabsorbowany przez cząstką przestrzeni lub cząstkę materii znajdującą się w punkcie C(x,y,z), przekaże do punktu materialnego pęd

.
 

Pęd przekazany do punktu materialnego w wyniku jego oddziaływania z przestrzenią i materią zawartą w pierścieniu jest

.
 

ha_wη² = G
 

Pęd przekazany do punktu materialnego w wyniku jego oddziaływania z cząstkami przestrzeni i cząstkami materii całego Wszechświata jest równy

.

Punkt materialny nie oddziałuje z cząstkami znajdującymi się w kuli K_P. W obliczeniach przyjęto, że punkt materialny oddziałuje z cząstkami przestrzeni i materii znajdującymi się w dowolnej odległości od niego. Wzór na pęd przekazany do punktu materialnego jest jednak poprawny, ponieważ wypadkowy pęd przekazany do punktu materialnego w wyniku oddziaływania z cząstkami kuli K_P (gdyby takie oddziaływanie istniało) jest wektorem zerowym.

Z obliczeń w "3.3. Siła działająca... wewnątrz materialnej kuli" otrzymujemy.

Siła działająca na punkt materialny P, o masie , jest równa

Wartość liczbowa tej siły jest równa

.

Na każde ciało materialne P, znajdujące się we Wszechświecie, działa siła grawitacji wywołana wzajemnym oddziaływaniem materii tego ciała z przestrzenią i pozostałą materią całego Wszechświata. Nazwijmy ją siłą RW (Rozciągającą Wszechświat). Zwrot tej siły jest zgodny ze zwrotem wektora . Nie biorę pod uwagę sił działających na to ciało ze względu na obecność innych ciał materialnych w pobliżu tego ciała. Analogiczna siła RW działa na cząstki przestrzeni.

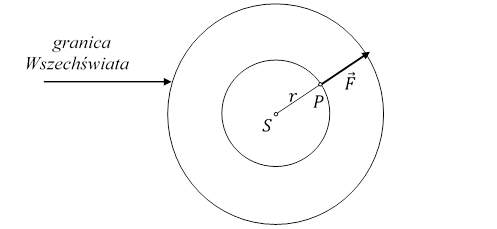
Rys. 4.1.2.

Siła działająca na punkt materialny ma zwrot wektora i stara się odsunąć punkt materialny od środka Wszechświata.

Przyspieszenie wywołane przez siłę RW jest równe

.
 

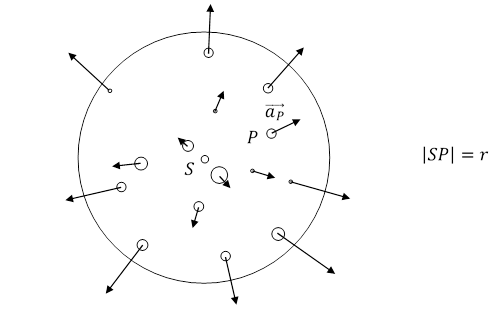
Rys. 4.1.3.

Przyspieszenie ciała P wywołane przez siłę RW jest wprost proporcjonalne do jego odległości r od środka S Wszechświata i ma zwrot wektora , ponieważ nie zerują się tylko siły pochodzące od przestrzeni i materii zawartej w kuli o środku S i promieniu r.

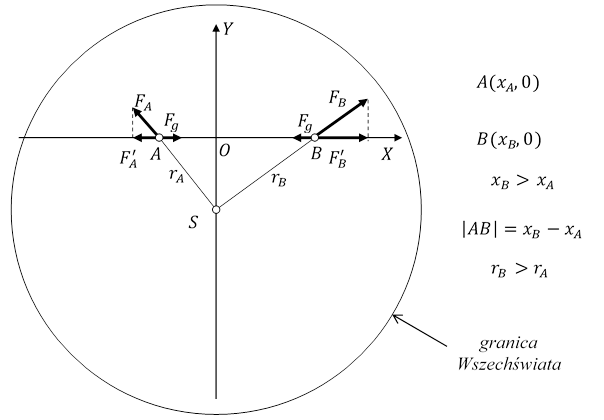
Rys. 4.1.4.

Weźmy dwa ciała materialne o masach i znajdujące się w punktach A i B takie, że

|AB| < d_w.

Oznaczmy przez i siły RW działające na te ciała. Na te ciała działają również siły wzajemnego “przyciągania” równe, co do wartości .

Współrzędne składowych wektorów i względem osi OX są odpowiednio

oraz

.

Współrzędne składowych wektorów przyspieszeń, względem osi OX, działających na ciała materialne znajdujące się w punktach A i B są odpowiednio

oraz

.

Jeżeli wówczas ciała będą się od siebie oddalały.

Siła wzajemnego “przyciągania” tych ciał

.

Siły i są określone następującymi wzorami.

Dzieląc obydwie strony nierówności przez otrzymujemy

.
 

Jeżeli odległość |AB| między materialnymi ciałami jest większa od

,

to ciała będą się od siebie oddalały nawet wtedy, gdy między nimi działają siły „przyciągania”.

Odległość |AB| zależy od średniej gęstości materii i przestrzeni we Wszechświecie, która nie jest dokładnie znana. Gdyby średnia gęstość materii i przestrzeni była 1000 razy mniejsza [większa], to odległość |AB| byłaby odpowiednio 10 razy większa [mniejsza].

Przyjmuję, że średnia gęstość materii i przestrzeni jest

.

Gdyby średnia gęstość materii i przestrzeni była równa gęstości wody, to odległość |AB| zmniejszy się trzy miliardy razy.

Oszacujemy odległość, przy jakiej przestaje działać siła „przyciągania” dla dwóch gromad galaktyk. Niech w każdej gromadzie znajduje się 5000 galaktyk. Przyjmuję, że każda galaktyka ma masę równą 10¹¹ mas Słońca. Masa jednej gromady galaktyk m = 5⋅10³⋅10¹¹⋅2⋅10³⁰ kg = 10⁴⁵.

|AB| > 1,68⋅10²⁴m
 

|AB| > 178 milionów lat świetlnych

Jeżeli odległość między tymi gromadami galaktyk przekroczy 178 milionów lat świetlnych to zaczną się od siebie oddalać nawet, jeśli początkowo były względem siebie w spoczynku. Dla takiej odległości między tymi gromadami siły RW przeważają nad siłami „przyciągania” grawitacyjnego. Ten wynik jest zgodny z danymi astronomicznymi (siły grawitacji przestają działać między gromadami galaktyk dla odległości większej niż 10²⁴ m). Jeżeli

|AB| > d_w,

to między ciałami nie ma „przyciągania” i na gromady galaktyk działają tylko siły RW.

Jeżeli gromady galaktyk są rozmieszczone równomiernie w przestrzeni, to siły „przyciągania” grawitacyjnego mogą się wzajemnie anulować, co spowoduje oddalanie tych gromad, nawet wtedy, jeżeli ich wzajemne odległości są znacznie mniejsze niż 178 milionów lat świetlnych.

Dla dwóch galaktyk o masie

m = 10¹¹⋅2⋅10³⁰ kg = 2⋅10⁴¹ kg

każda, odległość

|AB| > 9,85⋅10²²m = 10,4 milionów lat świetlnych.

Dla dwóch gwiazd o masie

m = 2⋅10³⁰ kg

każda, odległość

|AB| > 2,12⋅10¹⁹m = 2243 lat świetlnych.

Obliczenia dotyczą sytuacji, gdy dwa ciała znajdują się daleko od innych ciał. Jeżeli między dwiema gwiazdami z ostatniego przykładu znajdzie się trzecia o takiej samej masie to między nimi działają siły „przyciągania” i gwiazdy nie będą się od siebie oddalały.

Jeżeli ciała znajdują się blisko siebie to różnica między siłami RW działającymi na nie jest niewielka i przeważają siły “przyciągania” tych ciał. Przy dużych odległościach ciał materialnych siły “przyciągania” tych ciał są słabsze od sił RW, z jakimi przestrzeń i materia Wszechświata na nie oddziałuje i ciała oddalają się od siebie. Równocześnie cząstki materii i cząstki przestrzeni w podobny sposób oddziałują na fragmenty przestrzeni, skutkiem czego przestrzeń również się rozszerza.

Przestrzeń tak jak i materia ma niezerową masę, wobec czego nie może się rozszerzać z prędkością większą od prędkości światła. Ostatecznie siły grawitacji powodują rozszerzanie się Wszechświata przy zachowaniu stabilności układów ciał w mniejszej skali.

W wyniku oddziaływania grawitacyjnego we Wszechświecie mogą powstać obszary o gęstości przestrzeni większej od średniej (podobnie jak obszary materii o większej gęstości).

Jeżeli z jednej strony gromady galaktyk znajduje się obszar przestrzeni o dużej gęstości, to na tę gromadę działa siła „przyciągania” pochodząca z tego obszaru przestrzeni. Dlatego taka gromada galaktyk może poruszać się z pewną prędkością w stosunku do innych gromad znajdujących się daleko od tego obszaru przestrzeni.

Dla odległości dostatecznie dużych (siły przyciągania grawitacyjnego są bardzo słabe) przyspieszenie gromad galaktyk względem środka Wszechświata jest równe

.

Z takim samym przyspieszeniem rozszerza się przestrzeń.

Przyrost prędkości ciała P, wywołany siłą RW, znajdującego się daleko od innych ciał materialnych, po upływie czasu Δt jest równy

Δv = αΔt.

Dla ustalonej wartości Δt przyrost prędkości

jest wprost proporcjonalny do odległości ciała P od środka Wszechświata.

W obecnej chwili prędkość początkowa jest wprost proporcjonalna do odległości ciała od środka Wszechświata.

Dla dowolnych wartości Δt prędkości gromad galaktyk pozostaną wprost proporcjonalne do ich odległości od punktu S. To samo oczywiście powie każdy obserwator znajdujący się w dowolnym miejscu Wszechświata.

W obe­cnym czasie Wszechświat jest prawie płaski i rozszerza się w tym samym tempie we wszystkich kierunkach. Odpychające działanie grawitacji powoduje przyspieszenie ekspansji Wszechświata. Jest to zgodne z faktem wzrostu prędkości rozszerzania się Wszechświata. Obserwowane zjawisko przyśpieszenia ekspansji Wszechświata w prosty sposób wynika z istnienia sił RW.

Siła RW jest wprost proporcjonalna do średniej gęstości materii. W miarę upływu czasu średnia gęstość maleje, wobec tego wartość siły RW również się zmniejsza. Przyspieszenie ekspansji Wszechświata z czasem jest coraz mniejsze. Prędkość rozszerzania rośnie coraz wolniej. Nie musimy wprowadzać teorii inflacyjnej ani zakładać istnienie pól skalarnych dla wyjaśnienia obecnego stanu Wszechświata. Po prostu obecny stan Wszechświata jest skutkiem oddziaływania grawitacyjnego.

Ponieważ prędkość oddalania się ciał wzrasta z czasem wobec tego wiek Wszechświata jest większy niż wynikałoby to z obliczeń przyjmujących, że rozszerzanie zachodzi ze stałą prędkością równą obecnej prędkości rozszerzania się Wszechświata (Rys. 4.1.5.).

Wydaje się, że przedstawiony model oddziaływań grawitacyjnych usuwa problem istnienia gwiazd starszych od całego Wszechświata.

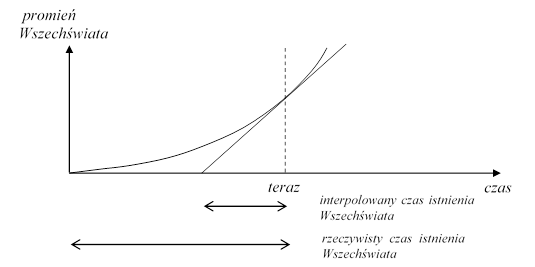
Rys. 4.1.5.

Siła RW jest określona wzorem

.

Można ją również zapisać, jako

,

gdzie

jest masą materii i przestrzeni znajdującej się w kuli K(S,r) o środku S i promieniu r. Ostatni wzór jest analogiczny do wzoru Newtona dla prawa powszechnej grawitacji, jednak siła skierowana jest nie do środka S, ale w przeciwną stronę.

Materia i przestrzeń, zawarta w kuli K(S,r), stara się odepchnąć cząstki materii oraz cząstki przestrzeni od środka Wszechświata S.

Wartość siły RW została obliczona przy założeniu, że w dużej skali średnia gęstość materii i przestrzeni jest taka sama w każdym miejscu Wszechświata. Przypuśćmy, że średnia gęstość przestrzeni oraz materii maleje w miarę oddalania się od środka S Wszechświata. Niech na przykład

,

gdzie jest gęstością materii i przestrzeni w centrum Wszechświata, R jest promieniem Wszechświata i r jest odległością od S. Wówczas masa materii oraz przestrzeni w kuli o środku S i promieniu r jest

.
 

Siła RW obliczona wcześniej jest równa

.

W rozpatrywanym przypadku

.

Siła RW w tym przypadku rośnie wolniej niż proporcjonalnie do r, wobec tego tempo rozszerzania obszaru Wszechświata w odległości r od S maleje ze wzrostem r. Obszary o większej gęstości rozszerzałyby się szybciej niż obszary o mniejszej gęstości. W rezultacie łączna gęstość materii i przestrzeni w różnych obszarach z czasem stałaby się jednakowa.

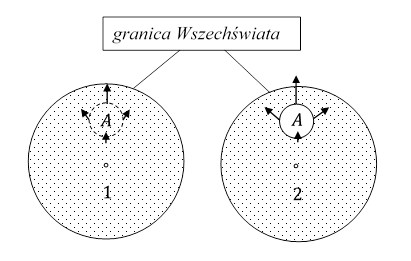
Rys. 4.1.6.

Weźmy obszar A dostatecznie duży (Rys. 4.1.6.), w którym siły RW mogą przezwyciężyć „przyciągające” siły grawitacji. W przypadku 1 gęstość materii w tym obszarze jest taka sama jak w pozostałych częściach Wszechświata. Wówczas ten obszar powiększa się w takim samym tempie jak reszta Wszechświata.

W przypadku 2 gęstość materii w obszarze A jest bardzo mała w stosunku do pozostałej części Wszechświata. Do jego brzegu dochodzi więcej grawitonów niż w przypadku pierwszym, ze względu na niewielką ilość materii w tym obszarze. Ze względu na mniejszą gęstość materii grawitony są słabiej absorbowane podczas przejścia przez ten obszar. Dlatego siły RW działające na materię znajdującą się na brzegu tego obszaru są większe niż w przypadku 1. Obszar A w przypadku 2 rozszerza się szybciej niż odpowiedni obszar w przypadku 1.

Gdyby we wczesnym okresie rozwoju Wszechświata powstało dożo takich obszarów o bardzo małej gęstości materii, to obecny Wszechświat byłby podobny do kuli mydlanej piany. Puste pęcherzyki, materia skupiona na ich ściankach.

Obszary o większej gęstości materii niż średnia powiększają się wolniej niż obszary o gęstości średniej.