2.3. Zmiana energii punktu materialnego przy jego przesunięciu w polu grawitacyjnym materialnej kuli
Pole grawitacyjne jest niejednorodne, jeżeli gradient potencjału pola grawitacyjnego jest wektorem niezerowym w punktach przestrzeni. Pole grawitacyjne w otoczeniu materialnej kuli jest niejednorodne. W niejednorodnym polu grawitacyjnym, dla ustalonego obserwatora, w różnych punktach przestrzeni, w jednostce czasu, z cząstką na ogół oddziałują różne ilości grawitonów; ta sama cząstka może mieć różną energię wewnętrzną (masę) w różnych punktach przestrzeni. Dla obserwatora związanego z cząstką jej masa i energia wewnętrzna nie zależą od położenia w przestrzeni. Na cząstki materii, w niejednorodnym polu grawitacyjnym, działają siły grawitacji wynikające z asymetrii ilości grawitonów oddziałujących z cząstką z różnych kierunków przestrzeni. Cząstki materii oraz przestrzeni nieustannie wymieniają między sobą pęd i energię, za pośrednictwem grawitonów. Energia może być swobodnie przekazywana z ciał materialnych do cząstek przestrzeni oraz cząstek innych ciał materialnych i odwrotnie.
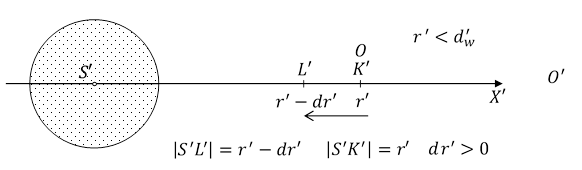
Rys. 2.3.1.
Obserwator O' znajduje się daleko od kuli, na osi S'X'. W obliczeniach używamy układu jednostek obserwatora O'. Obserwator O jest blisko punktu K'. Przesuńmy ruchem jednostajnym punkt materialny P o masie m', z punktu K' do punktu L', w polu grawitacyjnym kuli o masie 
i środku S'.
Wprowadźmy oznaczenia
i
.
Dla obserwatora O' masa punktu materialnego w punkcie K' jest równa
.
Zmiana masy punktu materialnego P podczas tego przesunięcia jest równa
.
Zmiana energii wewnętrznej podczas tego przesunięcia jest określona wzorem
.
Dla obserwatora O' siła
,
równoważąca siłą grawitacji, wykona pracę
.
Ponieważ
,
więc
dEw = dW
Dla obserwatora O' zmiana energii wewnętrznej punktu materialnego P, podczas jego przesunięcia z K' do L', jest dEw < 0. Również materialna kula zmieni swoją energię wewnętrzną o taką samą wartość jak i punkt materialny.
Podczas tego przesunięcia na ten punkt materialny działa zewnętrzna siła 
, równoważąca siłę grawitacji 
. Siła wykona pracę dW < 0, siła grawitacji - dEw.
Ponieważ oddziaływanie grawitacyjne zachodzi między punktem materialnym, kulą oraz materią i przestrzenią całego Wszechświata, należy rozpatrzyć zmiany energii układu - kula, punkt materialny, przestrzeń i pozostała materia. Jeżeli materialna kula jest nieruchoma i zbliżymy do niej punkt materialny, to kula absorbuje mniej grawitonów w jednostce czasu, zmniejsza swoją energię wewnętrzną, przekazując dodatnią energię - dEw do przestrzeni i pozostałej materii poprzez emisję grawitonów. Układ – kula, przestrzeń i pozostała materia nie zmieni swojej energii.
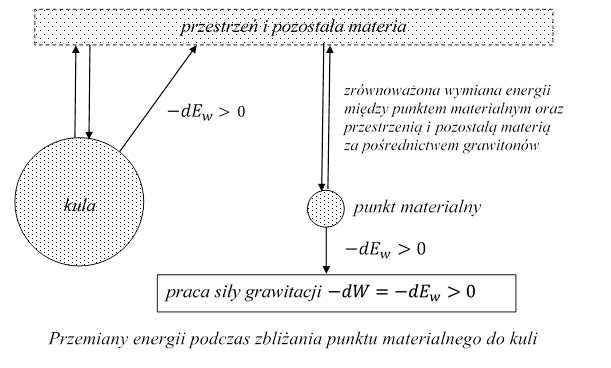
Rys. 2.3.2.
Od strony obserwatora O' z punktem materialnym oddziałuje więcej grawitonów niż od strony kuli. Siła grawitacji działająca na punkt materialny podczas tego przesunięcia wykonuje dodatnią pracę - dW, wykorzystując część energii absorbowanych grawitonów. Zmiana energii układu - punkt materialny, kula, przestrzeń i pozostała materia jest równa pracy
dW = dEw.
Punkt materialny przesuwa się do miejsca, w którym absorbuje mniej grawitonów, gdzie jego energia wewnętrzna jest mniejsza. Podczas tego przesunięcia punkt materialny emituje mniej grawitonów, niż absorbuje, ponieważ część energii absorbowanych grawitonów nie powiększa energii wewnętrznej tego punktu, ale służy do wykonania dodatniej pracy przez siłę grawitacji. W ten sposób punkt materialny zmniejsza swoją energię wewnętrzną przekształcając ją częściowo na pracę, wykonaną przez siłę grawitacji.
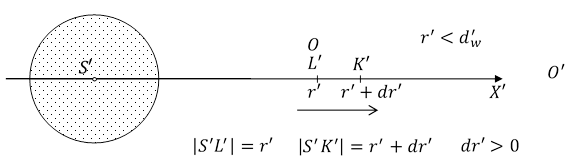
Rys.2.3.3.
Podczas przesunięcia punktu materialnego P z punktu L' do punktu K' zachodzi proces odwrotny, niż przy przesunięciu z K' do L'.
Kula absorbuje więcej grawitonów, niż emituje i w ten sposób pobiera z przestrzeni i pozostałej materii energię dEw > 0. Układ - kula oraz przestrzeń i pozostała materia nie zmienia swojej energii. Na punkt materialny działa siła zewnętrzna 
, wykonująca pracę dW > 0, przesuwając P do miejsca, w którym absorbuje więcej grawitonów, skutkiem czego zwiększa się jego energia wewnętrzna.
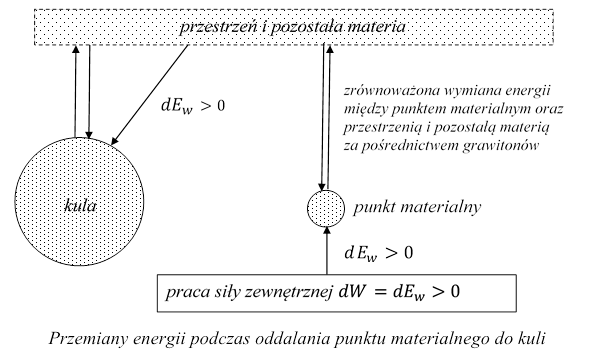
Rys.2.3.4.
Jeżeli punkt materialny P porusza się swobodnie od punktu K' do L', to zwiększa się jego pęd o wartość przekazaną przez grawitony z nim oddziałujące i równocześnie wzrasta jego energia kinetyczna, natomiast zmniejsza się jego spoczynkowa energia wewnętrzna Ew i pobierana jest dodatkowa energia z cząstek przestrzeni i pozostałej materii. Energia kinetyczna jest częścią całkowitej energii punktu materialnego. Zmiana energii kinetycznej punktu materialnego jest równa
dEk = - dEw.
Zmiana całkowitej energii tego punktu materialnego
dEk + dEw = 0.
Dla ruchu swobodnego z punktu L' do K' zachodzi proces odwrotny do poprzedniego.
Podczas dowolnego ruchu punktu materialnego prawdziwa jest zależność
dEk + dEw = dWF,
gdzie dWF jest pracą wykonaną przez zewnętrzną siłę działającą na punkt materialny. Jeżeli punkt materialny porusza się swobodnie, to
dWF = 0.
Podczas swobodnego spadku
.
W tym przypadku całkowita energia (masa bezwładna) swobodnie spadającego ciała jest stała. Taka sytuacja jest w przypadku ruchu planet dookoła Słońca.
Podczas ruchu jednostajnego zmiana energii wewnętrznej cząstki 
jest równa zmianie energii potencjalnej ciała 
, przy czym zmiana tej energii jest równa
dEw = dEp.
Tak wygląda mechanizm zamiany energii wewnętrznej ciała na energię kinetyczną lub pracę i odwrotnie, podczas ruchu ciała w statycznym polu grawitacyjnym. Istotne jest tu przesunięcie ciała z jednego punktu do drugiego, co powoduje zmianę ilość grawitonów absorbowanych przez to ciało. Drugim istotnym czynnikiem jest istnienie siły, dzięki której ciało zostaje przesunięte z jednego punktu do drugiego. Trzecim nieustanne przekazywania energii między ciałem oraz przestrzenią i pozostałą materią za pośrednictwem grawitonów.
Rys. 2.3.5.
Energia potencjalna punktu materialnego o masie m', względem kuli o masie , dla obserwatora O', jest równa pracy siły grawitacji podczas przesunięcia punktu materialnego z punktu O do O'.
Dla 
przybliżeniem jest klasyczny wzór
.