3.2. Siła grawitacji działająca na punkt materialny znajdujący się na zewnątrz materialnej kuli

Weźmy jednorodną materialną kulę o gęstości , objętości V_k, masie , promieniu d i środku S. W odległości r od środka S kuli umieśćmy punkt materialny P o masie (d < r < d_w). Zakładam, że masa punktu materialnego jest bardzo mała w stosunku do masy kuli, kula i punkt materialny są w spoczynku w układzie SXYZ oraz że punkt materialny P i kula znajdują się w bardzo dużej odległości od innych ciał materialnych. Masy, odległość i czas są mierzone przez obserwatora O znajdującego się blisko punktu materialnego P. Układ SXYZ nie jest układem inercjalnym.

Bez obecności kuli suma pędów przekazanych punktowi materialnemu przez grawitony z nim oddziałujące, w czasie Δt, byłaby wektorem zerowym. Z punktem materialnym P, w czasie Δt, ze względu na obecność kuli oddziałuje mniej grawitonów od strony kuli niż ze strony przeciwnej. Suma pędów przekazanych przez grawitony oddziałujące z punktem P jest wektorem niezerowym skierowanym do środka kuli.

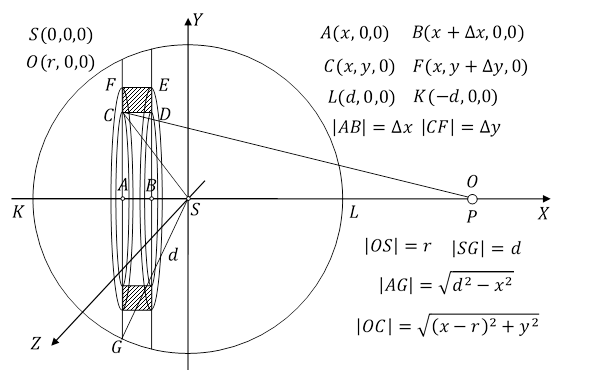
Rys. 3.2.1.

Weźmy pierścień kołowy utworzony przez obrót prostokąta CDEF dookoła osi OX. Objętość tego pierścienia jest równa

ΔV = 2πyΔyΔx

a jego masa

Obecność materii w pierścieniu powoduje, że punktowi materialnemu nie zostanie przekazany, w czasie Δt, pęd . Wobec tego pęd przekazany punktowi materialnemu przez grawitony z nim oddziałujące jest równy i skierowany w stronę środka kuli.

Podzielmy pierścień na parzystą ilość małych elementów ΔV mających równe objętości i masy.

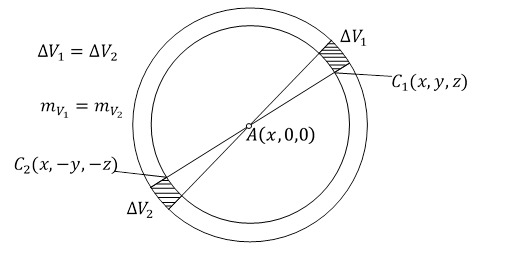
Rys. 3.2.2.

Pęd przekazany do punktu materialnego, ze względu na obecność materii o masie w elemencie ΔV₁ jest równy

gdzie

jest wektorem jednostkowym o zwrocie od punktu O do C₁ i punkt C₁(x,y,z) należy do elementu ΔV₁. Do każdego elementu ΔV₁ istnieje element ΔV₂ tego pierścienia o takiej samej objętości i masie, do którego należy punkt C₂(x,-y,-z), przy czym

|OC₁| = |OC₂| .

Pęd przekazany do punktu materialnego, ze względu na obecność materii o masie w elemencie ΔV₂ jest równy

gdzie

jest wektorem jednostkowym o zwrocie od punktu O do C₂.

Pęd przekazany do punktu materialnego ze względu na obecność materii w obydwu elementach jest równy

Pęd przekazany do punktu materialnego, ze względu na materię zawartą we wszystkich elementach pierścienia, jest równy

gdzie C jest odpowiednim punktem pierścienia.

Wektor ma zwrot od punktu materialnego do środka kuli, a jego wartość liczbowa jest równa

Wprowadźmy chwilowe oznaczenie

Wartość liczbowa całkowitego pędu przekazanego punktowi materialnemu ze względu na obecność kuli jest równa

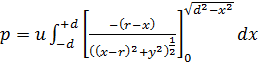
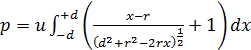
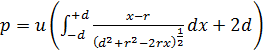
Do całki zastosujmy podstawienie

d² + r² - 2rx = t,

Górną granicę całkowania należy zmienić na

d² + r² - 2rd = (r - d)²

a dolną na

d² + r² + 2rd = (r + d)².

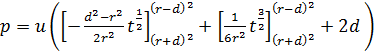
Ze względu na obecność kuli punktowi materialnemu P został przekazany pęd . Na punkt materialny działa siła określona wzorem

dla

Na punkt materialny P działa siła wprost proporcjonalna do iloczynu mas grawitacyjnych i m_k punktu materialnego i kuli oraz odwrotnie proporcjonalna do kwadratu odległości P od środka kuli. Zwrot tej siły jest zgodny ze zwrotem wektora . Efekt jest taki jak gdyby kula “przyciągała” punkt materialny. Wyprowadzony wzór jest analogiczny do wzoru określającego prawo powszechnej grawitacji Newtona. Porównując otrzymany wzór dla siły ze wzorem dla prawa powszechnej grawitacji Newtona

otrzymujemy zależność

G = a_whη²,

dla obserwatora O.

Kula znajdująca się w pewnej odległości od punktu materialnego powoduje zmianę ilości grawitonów oddziałujących z punktem materialnym. Podobnie, na podstawie Założenia 8, obecność punktu materialnego powoduje zmianę ilości grawitonów oddziałujących z kulą od strony punktu materialnego. Siła działająca na kulę, wynikająca z obecnością punktu materialnego, jest wektorem przeciwnym do siły działającej na punkt materialny.

Siła F „wzajemnego przyciągania” punktu materialnego i jednorodnej kuli o masach grawitacyjnych i m_k, umieszczonych w odległości r między ich środkami, jest wprost proporcjonalna do iloczynu mas grawitacyjnych tych ciał i odwrotnie proporcjonalna do kwadratu odległości między ich środkami.

Jeżeli przyjmiemy, że odległość między punktem materialnym i środkiem kuli jest równa odległości według współrzędnych, to siła działająca na punkt materialny nie zależy od objętości kuli, ale od jej masy.

Siła grawitacji działająca na punkt materialny P jest wynikiem jego oddziaływania z przestrzenią i materią znajdującą się w kuli oddziaływania grawitacyjnego, za pośrednictwem grawitonów.

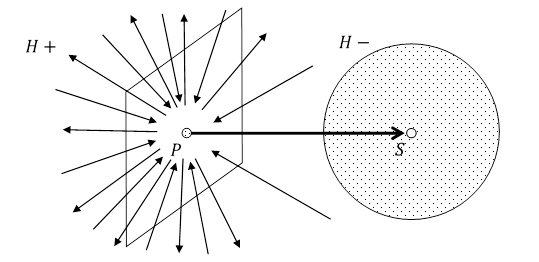
Rys. 3.2.3.

Płaszczyzna przechodząca przez punkt P i prostopadła do wektora (jak na Rys. 3.2.3.) dzieli przestrzeń na dwie półprzestrzenie. Przez H - oznaczmy tą półprzestrzeń, w której znajduje się wektor , a przez H + pozostałą półprzestrzeń. (H - jest tą półprzestrzenią, w której znajduje się kula o środku S).

Wniosek II.

Siła grawitacji działająca na punkt materialny P jest skutkiem tego, że z punktem materialnym P oddziałuje więcej grawitonów z półprzestrzeni H + niż z H - . Siła ta jest wprost proporcjonalna do masy grawitacyjnej tego punktu materialnego. Siła grawitacji, jak również siła bezwładności, działająca na punkt materialny P jest wynikiem braku symetrii oddziaływania tego punktu materialnego z cząstkami przestrzeni i materii, zawartymi w kuli oddziaływania grawitacyjnego.

Masa grawitacyjna ciała wynika z istnienia siły „przyciągania” działającej między ciałami. Masa bezwładna wynika z istnienia siły bezwładności działającej na ciało poruszające się ruchem zmiennym.

Masa grawitacyjna jak również masa bezwładna ciała są konsekwencją oddziaływania tego ciała z przestrzenią i materią całego Wszechświata zawartą w kuli oddziaływania grawitacyjnego, za pośrednictwem grawitonów.

Dla obserwatora O, siła „przyciągania” działająca między ciałami o masach m i M znajdującymi się w odległości r, jest określona wzorem

Dla obserwatora O' mamy

Siła grawitacji F jest zmierzona przez obserwatora O. Według tego obserwatora wartość tej siły dla obserwatora O' w miejscu O jest równa

Jeżeli siłę grawitacji zmierzy obserwator O', to otrzyma wartość

Wartości m', M' i r' są mierzone przez tego obserwatora. Stała grawitacji jest taka sama dla każdego obserwatora. F' ma w ostatnim wzorze inne znaczenie niż we wzorze poprzednim. Dla obserwatora O' siła grawitacji w miejscu gdzie znajduje się obserwator O jest równa

Weźmy kulę o masie M, środku S i promieniu R zachowującą się tak jak elementarna cząstka, to znaczy emitującą i absorbującą grawitony tylko na powierzchni. Punkt materialny (cząstka elementarna) o masie m znajduje się w punkcie P, na powierzchni kuli. Obserwator O znajduje się blisko punktu materialnego.

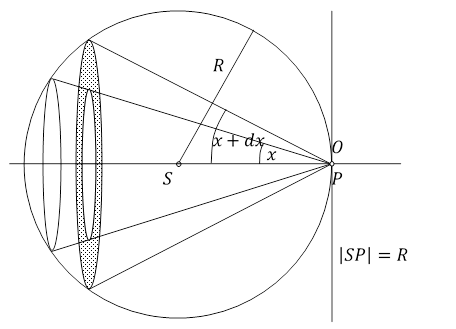
Rys. 3.2.4.

Kąt bryłowy określony przez kąt x ma miarę

;

kąt pełny ma miarę 4π. Do punktu materialnego nie dochodzą grawitony z półprzestrzeni, w której znajduje się kula, ograniczonej płaszczyzną styczną do kuli w punkcie P. Bez obecności kuli punkt materialny o masie m absorbuje, w czasie Δt, energię określoną wzorem (patrz 1.6.)

Stąd otrzymujemy

Z kąta bryłowego określonego przez kąt x do punktu materialnego nie dochodzi energia

Dla x + dx mamy odpowiednio

Ilość energii, która w czasie Δt, nie dochodzi do punktu materialnego z kąta bryłowego określonego przez x + dx, z którego wycięto kąt bryłowy określony przez x, jest równa .

Pęd, który nie zostanie przekazany do punktu materialnego, w czasie Δt, jest równy

a jego składowa równoległa do prostej SP jest równa

Całkowity pęd, który nie zostanie przekazany do punktu materialnego, jest równy

(patrz 1.7.)

Siła działająca na punkt materialny jest

nie zależy od masy kuli i jest największą siłą działającą na ciało o masie m. Dla bardzo dużych wartości gęstości kuli, złożonej z elementarnych cząstek, siła działająca na punkt materialny, znajdujący się na powierzchni tej kuli, jest niewiele mniejsza od F_max.

Weźmy punkt materialny o masie m znajdujący się na powierzchni kuli o masie M i promieniu R. Dla obserwatora O, związanego z punktem materialnym, masa punktu materialnego jest zmniejszona o

Ponieważ masa punktu materialnego może się zmniejszyć, co najwyżej do połowy, (do punktu materialnego nie dochodzi połowa grawitonów od strony kuli), więc

Jeżeli promień materialnej kuli jest równy

o ile taka wartość promienia jest możliwa dla kuli o masie M, to na punkt materialny znajdujący się na powierzchni kuli działa największa siła F_max, niezależna od masy kuli.

Gęstość materii kuli o promieniu w jest równa

Dla Słońca

m_S = 1,989⋅10³⁰ kg .

Gdyby r_S = w, to wtedy . Dla Słońca taka wartość gęstości jest niemożliwa. Słońce może się jedynie przekształcić w białego karła o znacznie mniejszej gęstości.

Jeżeli punkt materialny o masie m znajduje się na powierzchni kuli o masie M i promieniu

to według prawa powszechnej grawitacji działa na niego siła

Kula w tym przypadku jest podobna do cząstki elementarnej, masa takiej kuli jest proporcjonalna do jej powierzchni i jest określona wzorem

Masa kuli jest

Siła F_g obliczona według wzoru Newtona jest dwa razy mniejsza od siły F_max. Prawo Newtona nie jest prawdziwe w tym przypadku.

Jeżeli r > d_w, to między kulą i punktem materialnym nie działają siły „przyciągania” grawitacyjnego.