5.3. Maksymalna odległość punktu materialnego od Słońca podczas jego swobodnego ruchu po orbicie eliptycznej
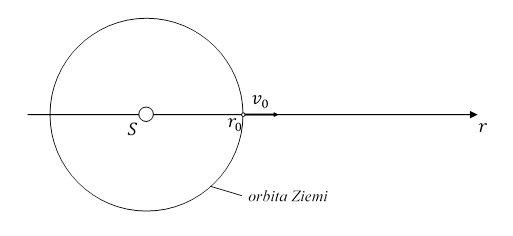
Rys. 5.3.1.
Weźmy punkt materialny znajdujący się w odległości r0 od Słońca, równej promieniowi orbity Ziemi. Wyrzućmy go w stronę przeciwną do Słońca z prędkością początkową 
. Obliczmy maksymalną odległość r na jaką punkt materialny oddali się od Słońca. Obliczenia przeprowadzę w dwóch przypadkach w zależności od przyjętego wzoru dla całkowitej energii tego punktu. Ze wzoru dla klasycznej całkowitej energii mamy
.
Po podstawieniu dla prędkości końcowej v wartości zero otrzymujemy
,
gdzie
i M jest masą Słońca. Po przekształceniu otrzymujemy następujące równanie.
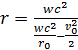
W przypadku wprowadzonej w tej książce zmodyfikowanej całkowitej energii otrzymujemy
.
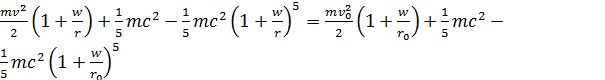Po podstawieniu v = 0 otrzymujemy bardziej skomplikowane, niż poprzednio, równanie.
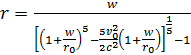
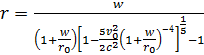
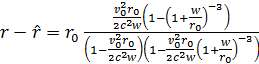
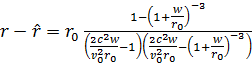
Do obliczeń przyjmuję następujące wielkości.
r0 = 1,49588⋅108 km
 | r |  | |
| 35 | 3,2286⋅r0 | 22,0 | |
| 38,5 | 6,0690⋅r0 | 113,8 | okolice orbity Jowisza |
| 40 | 10,1605⋅r0 | 372,7 | okolice orbity Saturna |
| 41,1 | 20,7676⋅r0 | 1 731,3 | okolice orbity Urana |
| 41,45 | 31,3761⋅r0 | 4 088,1 | okolice orbity Neptuna |
| 41,8 | 64,7131⋅r0 | 17 985,4 | |
| 42 | 166,4231⋅r0 | 121 242,0 | |
| 42,1 | 787,4927⋅r0 | 2 740 576,3 |
Ze wzrostem maksymalnej odległości, na jaką oddali się punkt materialny od Słońca szybko wzrasta różnica między zasięgiem rzutu punktu materialnego w rozpatrywanych przypadkach.
Zasięg rzutu jest równy odległości od Słońca punktu materialnego w aphelium ra podczas jego ruchu po orbicie eliptycznej, przy jednakowej szybkości początkowej v0 i takiej samej odległości r0 od Słońca.
Rys. 5.3.2.
Odległość punktu materialnego w aphelium jest większa dla orbity newtonowskiej, niż dla orbity wynikającej z zastosowania nowego wzoru dla energii potencjalnej, przy tych samych warunkach początkowych. Sonda kosmiczna wyrzucona z orbity Ziemi oddali się na mniejszą odległość od Słońca, niż wynika to z obliczeń, w których stosujemy prawa ruchu Newtona.