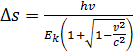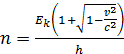1.2. Ruch elementarnej cząstki materii lub przestrzeni

W rozdziale 1 przyjmuję minimalną liczbę koniecznych założeń, z których wynika istnienie grawitacji i bezwładności ciał zgodnie ze znanymi faktami potwierdzonymi doświadczalnie.

W mechanice klasycznej i kwantowej przyjmuje się, że ruch elementarnej cząstki jest ciągły, ale to jest tylko założenie. Gdyby elementarna cząstka poruszała się w ten sposób w układzie inercjalnym, wówczas, jak można obliczyć, byłaby hamowana w wyniku jej oddziaływania z grawitonami. Tego w rzeczywistości nie obserwujemy. W układzie inercjalnym cząstka porusza się ruchem jednostajnym. Dlatego powinniśmy zmodyfikować sposób, w jaki poruszają się cząstki elementarne.

Założenie 1.

Wszechświat zbudowany jest z materii i przestrzeni. Przestrzeń (próżnia) tak jak i materia ma budowę cząsteczkową, tzn. przestrzeń nie jest ciągła, lecz jest zbudowana z dyskretnych elementów – cząstek elementarnych.

We Wszechświecie istnieje jeden wyróżniony układ odniesienia UW (z dokładnością do przesunięcia i obrotu), w którym ruch cząstki elementarnej ma szczególny charakter. W niektórych miejscach przestrzeni układ UW może być układem lokalnie inercjalnym, dla obserwatora O, w innych nie.

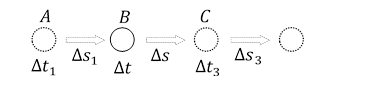
Rys. 1.2.1.

Ruch każdej elementarnej cząstki materii lub cząstki przestrzeni, w układzie UW, nie jest ciągły, ale odbywa się w sposób skokowy. Cząstka w czasie Δt₁ spoczywa w określonym miejscu A przestrzeni a następnie momentalnie, w chwili t₁, przenosi się w inne miejsce B. Znika w miejscu A i pojawia się w miejscu B. Pozostaje w spoczynku w punkcie B, w czasie Δt a następnie przenosi się momentalnie do miejsca C, wykonując skok na odległość Δs i tak dalej. Czas spoczynku Δt w miejscu B jest równocześnie odstępem czasu między skokiem z B do C. Przez prędkość cząstki (w zwykłym znaczeniu tego pojęcia), w układzie UW, rozumiem wielkość

.

Należy jednak zdawać sobie sprawę, że cząstka w układzie UW cały czas pozostaje w spoczynku, niezależnie od jej prędkości v, wykonując jedynie momentalne skoki z jednego punktu do drugiego.

Elementarna cząstka materii oraz przestrzeni podczas spoczynku w układzie UW posiada pewien pęd, który określa odstęp czasu między skokami oraz długość i kierunek skoku. Zwrot wektora przesunięcia

jest zgodny ze zwrotem wektora pędu cząstki w chwili wykonywania skoku z punktu B do C.

Podczas skoku z jednego miejsca do drugiego położenie cząstki jest nieokreślone i cząstka nie oddziałuje z innymi cząstkami materii lub przestrzeni. Zmiana pędu i energii kinetycznej cząstki może nastąpić tylko wtedy, gdy cząstka pozostaje w spoczynku w układzie UW. Jeżeli z dowolnych przyczyn zmieni się pęd i energia cząstki, to odpowiednio zmieni się długość skoku, czas między jednym a drugim skokiem i wektor jej skoku.

W wyróżnionym układzie odniesienia UW, po wykonaniu skoku, z punktu A do B, cząstka pozostaje w spoczynku w punkcie B w czasie Δt, w zależności od jej masy spoczynkowej (grawitacyjnej) m₀ i pędu p jaki posiada w tym układzie. Pęd cząstki p = p(t) w czasie spoczynku w punkcie B może się zmieniać w zależności od czasu t, liczonego od chwili skoku do punktu B. Na przykład, jeżeli elektron znajduje się w polu elektrycznym.

Po wykonaniu każdego skoku zaczynamy odliczać czas od zera.

Prędkość cząstki

v = v(t)

w zależności od pędu p jest określona wzorem

.

Niech

,

gdzie

.

Jeżeli

            ,

to cząstka pozostaje w spoczynku w punkcie B. Skok z punktu B do C następuje w chwili

t = Δt,

gdy iloczyn

            ,

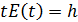
gdzie h jest stałą Plancka.

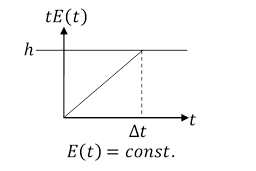
Czas t = Δt po jakim następuje skok z jednego punktu do drugiego jest najmniejszym rozwiązaniem równania tE(t) = h.

Rys. 1.2.2.

Czas spoczynku Δt w punkcie B (odstęp czasu między kolejnymi skokami)

.

,

gdzie

p = p(Δt)

jest pędem cząstki w chwili skoku z punktu B do C.

jest długością jednego skoku cząstki.

Długości skoków

|AB| = Δs₁,

|BC| = Δs, …

są odwrotnie proporcjonalne do pędu cząstki w tym układzie, w momencie skoku.

.

Ruch cząstki w układzie UW jest podobny do ruchu falowego. Jeżeli przyjmiemy,

λ = vΔt

jako długość tej fali, to

.

λ = Δs

Częstotliwość tego ruchu

.

,

gdzie E_k jest energią kinetyczną cząstki.

.

Dla małych prędkości, w porównaniu z prędkością światła otrzymujemy.

p = m₀v

Dla małej prędkości czas spoczynku cząstki Δt jest odwrotnie proporcjonalny do jej energii kinetycznej natomiast ilość skoków n, jakie wykonuje cząstka w jednostce czasu, jest wprost proporcjonalna do jej energii kinetycznej.

Ponieważ , więc prędkość cząstki nie może być większa lub równa od prędkości światła.

Ruch elementarnej cząstki materii wydaje się ciągły, ponieważ odległość, na jaką jest wykonywany skok jest bardzo mała i odstęp czasu między kolejnymi skokami jest bardzo krótki. Wprowadzony sposób ruchu cząstek elementarnych będzie może mniej dziwny, jeżeli zauważymy, że cząstka w swoim ruchu wykazuje własności falowe. Istnienie fali związanej z ruchem materialnej cząstki jest potwierdzone doświadczalnie.

Dla elektronu, w układzie UW, długość skoku, czas między jednym a drugim skokiem i częstotliwość skoków, w zależności od prędkości, są określone w następującej tabeli.

1	7,3⋅10-4	7,3⋅10-4	1,4⋅103
103	7,3⋅10-7	7,3⋅10-10	1,4⋅109
106	7,3⋅10-10	7,3⋅10-16	1,4⋅1015

Na ruch elementarnej cząstki należy spojrzeć w nowy sposób. Dotychczas przyjmowałem, że cząstka ma pewien pęd, ponieważ się porusza. W rzeczywistości jest odwrotnie: cząstka się porusza, ponieważ ma określony pęd.

Energia kinetyczna cząstki jest określona jednoznacznie za pomocą pędu i masy spoczynkowej.

Weźmy prostokątny układ współrzędnych OXYZ, który spoczywa, w inercjalnym ukła­dzie UW.

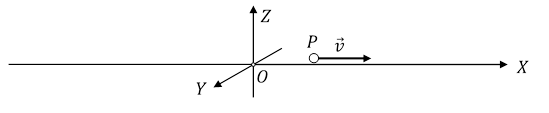
Rys. 1.2.3.

Niech cząstka P porusza się ruchem jednostajnym z prędkością po osi OX, zgodnie z jej zwrotem. Dla obserwatora O położenie x tej cząstki w zależności od czasu t jest pokazane na Rys. 1.2.4..

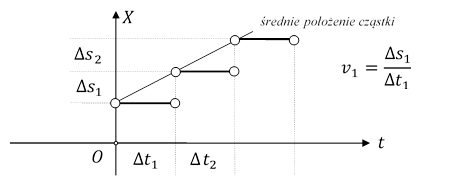
Rys. 1.2.4.

Niech prostokątny układ współrzędnych O'X'Y'Z' porusza się z prędkością względem układu OXYZ tak, że oś O'X' porusza się po osi OX zgodnie z jej zwrotem, przy czym w < v.

Rys. 1.2.5

Rys. 1.2.6.

Dla obserwatora O' położenie cząstki zmienia się tak, jak na Rys. 1.2.6..

Ruch elementarnej cząstki w układzie O'X'Y'Z' jest również serią skoków, ale między jednym a drugim skokiem cząstka nie spoczywa w tym układzie, lecz w układzie UW. Dla obserwatora O' związanego z układem O'X'Y'Z' długości skoków oraz czasy spoczynku między skokami, mogą być inne niż w UW, ale są zgodnie ze Szczególną Teorią Względności.

Niech obserwator O' porusza się z prędkością w = v.

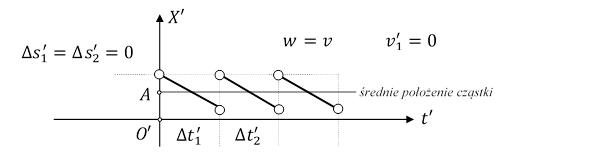
Rys. 1.2.7.

Dla takiego obserwatora O' cząstka wykonuje pewien rodzaj oscylacji względem stałego punktu A w układzie O'X'Y'Z'.

W układzie poruszającym się względem układu UW spoczynek cząstki elementarnej jest niemożliwy.

Rys. 1.2.8.

Niech cząstka elementarna porusza się ruchem jednostajnym wzdłuż prostej l, która porusza się ruchem jednostajnym, z prędkością , względem układu UW. Po wykonaniu skoku cząstka znajdzie się w punkcie P na prostej l. Następnie przesuwa się ruchem jednostajnym o wektor do punktu Q (w wyniku ruchu jednostajnego prostej l względem układu UW, w którym ta cząstka pozostaje w spoczynku), potem wykonuje skok o wektor powracając na prostą l do punktu R. Jeżeli cząstka poruszając się w dalszym ciągu po prostej zmniejsza [zwiększa] prędkość, to długości wektorów i w kolejnych skokach stają się odpowiednio większe [mniejsze].

Cząstki elementarne, wchodzące w skład cząstek złożonych, poruszają się skokowo, ale ze względu na wzajemne oddziaływanie (elektromagnetyczne, jądrowe) poruszają się średnio, w większych odstępach czasu, z jednakową prędkością. W bardzo małych odstępach czasu cząstki elementarne, w cząstce złożonej, poruszają się względem siebie ze stale zmieniającymi się prędkościami. Spoczynek cząstek elementarnych tworzących cząstkę złożoną jest niemożliwy.

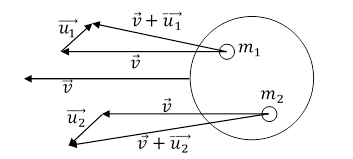
Rys. 1.2.9.

Weźmy cząstkę złożoną z dwóch cząstek elementarnych o masach m₁ i m₂. Niech cząstka, jako całość porusza się z prędkością w układzie UW. Ze względu na wzajemne oddziaływanie cząstek elementarnych ich prędkości są odpowiednio oraz .

Suma pędów cząstek elementarnych jest równa

.

Ponieważ prędkości i wynikają ze wzajemnego oddziaływania cząstek elementarnych, więc .

Pęd cząstki, jako całości jest równy

.

Wektory i są równoległe i mają zgodne zwroty, więc

p = p₁ = p₂.

Δs₁ i Δs₂ są długościami skoków cząstek elementarnych i Δs jest długością skoku cząstki. Gdyby cząstki elementarne miały równe masy wówczas

Δs₁ = Δs₂

i

.

Dla n cząstek elementarnych tworzących cząstkę złożoną mamy

i odpowiednio

.

Cząstki elementarne o bardzo małym pędzie i bardzo małej energii kinetycznej, w układzie UW, mogą wykonywać skoki na duże odległości pod warunkiem, że zachowają ten pęd i tą energię kinetyczną przez dostatecznie długi odstęp czasu. Cząstki elementarne w jądrze atomowym również poruszają się skokowo. Jeżeli cząstka elementarna w jądrze atomu uzyska przypadkiem bardzo mały pęd, w układzie UW, to niekiedy może wykonać skok na taką odległość, że znajdzie się poza sferą oddziaływania jądra.

Niech elektron porusza się z malejącą prędkością. Podczas pierwszego skoku miał energię kinetyczną E_k1. Przed wykonaniem tego skoku pozostawał w spoczynku w czasie

.

Następny skok wykona z energią kinetyczną E_k2 < E_k1 po upływie czasu

.

Różnicę energii E_k1 - E_k2 emituje w postaci kwantu promieniowania elektromagnetycznego z częstotliwością v₂.

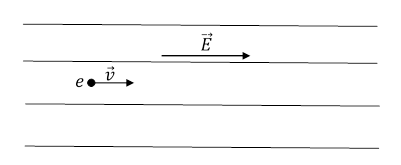
Rys. 1.2.10.

Elektron porusza się w polu elektrycznym o natężeniu , równolegle do linii siły tego pola, jak na rysunku powyżej.

Na elektron działa siła

zmniejszająca jego prędkość. Opóźnienie z jakim porusza się elektron jest równe

.

Po wykonaniu skoku, w pewnej chwili, prędkość elektronu jest równa v₀. Weźmy funkcję

E(t) = m_e(v₀ - at)² .

Następny skok następuje w chwili t w której

.

tm_e(v₀ - at)² = h

Oznaczmy

D(t) = tm_e(v₀ - at)²

dla

.

D(0) = 0

Funkcja D(t) ma maksimum dla

a jej wartość

.

Rys. 1.2.11.

Jeżeli

,

to skok elektronu nastąpi po czasie

.

Ten warunek jest spełniony gdy

.

Oznaczmy

.

Weźmy

.

Wówczas

.

Niech

.

Czas t₁ po jakim zostanie wykonany pierwszy skok jest mniejszym rozwiązaniem równania

tm_e(v₀ - at)² - h = 0

w przedziale

.

t(v₀ - at)² - 7,273895032⋅10^-4 = 0

dla

.

Prędkość v₁ po wykonaniu tego skoku jest równa

v₁ = v₀ - at₁ .

Czas t_k, dla k = 1, 2, 3, …, po jakim zostaną wykonane następne skoki jest mniejszym rozwiązaniem równania

tm_e(v_k-1 - at)² - h = 0

w przedziale

.

Prędkość v_k po wykonaniu tego skoku jest równa

v_k = v_k-1 - at_k .

Po wykonaniu skoku elektron emituje foton którego częstotliwość obliczamy ze wzoru

lub

.

k	tk[s]
0		3⋅107
1	9,008544328935⋅10 -19	2,841555905⋅10 7	6,362⋅10 16
2	1,02734375⋅10 -18	2,660864614⋅10 7	6,834⋅10 16
3	1,21453637695313⋅10 -18	2,447249506⋅10 7	7,501⋅10 16
4	1,53421926879885⋅10 -18	2,177497925⋅10 7	8,578⋅10 16
5	2,32640624999999⋅10 -18	1,768234900⋅10 7	1,110⋅0 17

Po wykonaniu piątego skoku nie jest spełniony warunek

.

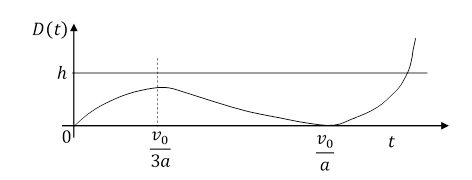
Rys. 1.2.12.

Jeżeli

,

to w czasie

skoku nie będzie. Wektor pędu elektronu zmieni zwrot na przeciwny i skok nastąpi po czasie

w stronę przeciwną do poprzedniego skoku.

Czas t po jakim nastąpi skok jest jedynym rozwiązaniem równania

.

dla

t > 1,005352864⋅10^-17 s.

Rozwiązaniem jest

t = 1,41325000000004⋅10^-17 s.

Prędkość elektronu po wykonaniu skoku jest równa

.

Ponieważ v₆ > v₅ więc elektron nie wyemituje fotonu, zostanie jedynie odrzucony w przeciwną stronę, pobierając pewną energię z pola elektrycznego.

Podczas kolejnych pięciu skoków częstotliwość emitowanych kwantów jest coraz większa. Obliczone wartości v_k wynikają w prosty sposób z przyjętego założenia, że elementarne cząstki poruszają się w sposób skokowy.

Gdyby elektron poruszał się w sposób ciągły to jak wytłumaczyć emisję fotonów w postaci określonych porcji energii.

Wykonując odpowiednie doświadczenie z hamowaniem elektronu w polu elektrycznym moglibyśmy się przekonać, czy założenie o skokowym ruchu cząstek elementarnych jest prawdziwe.

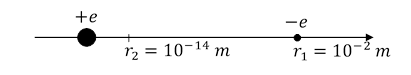
Rys. 1.2.13.

Elektron spada na proton z odległości r₁ r₂ na odległość. (Rys. 1.2.13.)

Jeżeli początkowa energia kinetyczna jest równa zero, to końcową możemy obliczyć ze wzoru

.

Prędkość końcowa elektronu

.

Dla podanych odległości

.

Jeżeli elektron porusza się z taką prędkością, to wykonuje skoki o długości

.

W tym przykładzie elektron znajdzie się po drugiej stronie protonu. Dalej elektron wykona kilka skoków tracąc energię kinetyczną przez promieniowanie, następnie wykona kilka skoków lub jeden skok w stronę protonu i znajdzie się po jego drugiej stronie. Ostatecznie elektron będzie przeskakiwał z jednej strony protonu na drugą zachowują jednakową odległość z każdej strony. Również proton będzie wykonywał skoki, ale ze względu na jego dużą masę w stosunku do elektronu, można je pominąć. Przypuszczam, że prawdopodobieństwo trafienia elektronu w proton jest bardzo małe i praktycznie nie występuje.

To, że elektron nie spada na proton jest wnioskiem z przyjętego założenia o skokowym charakterze ruchu cząstek elementarnych.

Rys. 1.2.14.

Obliczmy odległość r dla której elektron, o masie m będzie przeskakiwał z jednej strony protonu na drugą przy zachowaniu odległości od niego. Do odpowiednich równań zamiast h podstawmy

dla

n = 1, 2, 3, … .

Czas t po którym nastąpi skok obliczmy z równania

.

Odległość jest zachowana gdy

.

Długość skoku 2rr obliczamy ze wzoru

.

Z tych trzech równań otrzymujemy

,

,

,

energia kinetyczna elektronu podczas przeskoku

,

energia potencjalna w odległości rr_n jest równa

,

energia całkowita

.

r_n i E_n są znanymi wartościami obliczonymi z modelu atomu wodoru Bohra, ale tutaj są wynikiem założenia o skokowym charakterze ruchu cząstek elementarnych. Odległość elektronu od protonu r₁ = 5,292⋅10^-11 m. Czas po jakim następuje przeskok elektronu t₁ = 4,838⋅10^-17 s.

Po każdym skoku, przy zachowaniu odległości, elektron ma taką samą energię kinetyczną i potencjalną a więc nie traci energii przez promieniowanie. Atom wodoru możemy sobie wyobrazić jako układ złożony z protonu i elektronu przeskakującego z jednej strony protonu na drugą.

Dla obserwatora związanego z cząstką prędkość światła dochodzącego do cząstki jest taka sama niezależnie od prędkości, z jaką porusza się ta cząstka. Jeżeli zmierzymy prędkość fotonu poruszającego się blisko cząstki, w czasie jej spoczynku w układzie UW, to dla każdej takiej cząstki prędkość tego fotonu jest taka sama i równa c, niezależnie od prędkości v tej cząstki względem układu UW.

Wykonajmy następujące doświadczenie.

Rys. 1.2.15.

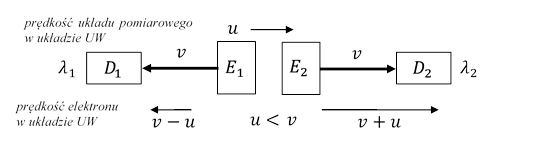
Z urządzeń E₁ i E₂ są emitowane w przeciwne strony, z jednakową szybkością v, elektrony. Następnie te elektrony trafiają do detektorów D₁ i D₂, które mierzą odpowiednie długości fal λ₁ i λ₂ tych elektronów. Detektory D₁ i D₂ oraz emitery E₁ i E₂ leżą na prostej k. Pomiary należy powtarzać przy różnym ustawieniu układu pomiarowego w przestrzeni. Jeżeli jesteśmy w układzie UW, to podczas tych pomiarów elektrony, poruszające się w przeciwne strony, będą miały te same prędkości względem układu UW i odpowiednio równe, odpowiadające im, długości fal. Jeżeli przy pewnym ustawieniu układu pomiarowego elektrony poruszające się w przeciwne strony mają różne długości fal (), to znaczy, że ten układ pomiarowy porusza się względem układu UW. Różnice długości tych fal będą największe, jeżeli elektrony poruszające się w jedną stronę będą miały prędkość porównywalną z prędkością układu pomiarowego względem układu UW oraz gdy prosta k jest równoległa do wektora . Jeżeli prosta k jest prostopadła do wektora , to .

Niech układ pomiarowy porusza się z prędkością , równoległą do prostej k, względem układu UW.

Rys. 1.2.16.

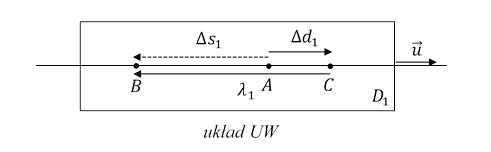
Niech w układzie UW elektron po wykonaniu skoku znajdzie się w punkcie A. Następny skok wykona na odległość

i znajdzie się w punkcie B, po upływie czasu

.

W tym czasie detektor D₁ przesunie się o

.

Rys. 1.2.17.

Według obserwatora związanego z detektorem D₁ elektron po wykonaniu skoku znalazł się w punkcie P, następnie poruszał się ruchem jednostajnym do punktu Q i z tego punktu wykonał skok do punktu R. W efekcie przesunął się na odległość

λ₁ = Δs₁ + Δd₁ .

Rys. 1.2.18.

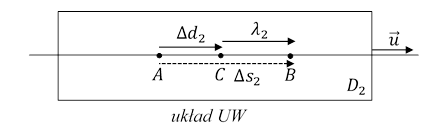
W układzie UW elektron po wykonaniu skoku znajdzie się w punkcie A. Następny skok wykona na odległość

i znajdzie się w punkcie B, po upływie czasu

.

W tym czasie detektor D₂ przesunie się o

.

Rys. 1.2.19.

Dla obserwatora związanego z detektorem D₂ elektron po wykonaniu skoku znalazł się w punkcie P, następnie poruszał się ruchem jednostajnym do punktu Q i z tego punktu wykonał skok do punktu R. W efekcie przesunął się na odległość

λ₂ = Δs₂ + Δd₂ .

Być może układ odniesienia UW spoczywa względem mikrofalowego kosmicznego promieniowania tła (CMB). Ziemia porusza się względem CMB w przybliżeniu z prędkością . Jeżeli tak jest rzeczywiście, to swobodny elektron, spoczywający względem Ziemi, wykonuje w przybliżeniu rodzaj drgań z częstotliwością i amplitudą 1,2⋅10^-9 m. Każda elementarna cząstka znajdująca się w pobliżu innych cząstek wykonuje, względem Ziemi, chaotyczne ruchy ze zmienną częstotliwością i amplitudą. W układzie poruszającym się względem układu UW spoczynek cząstki elementarnej jest niemożliwy.

Jeżeli i elektron porusza się z prędkością , to λ₁ - λ₂ = 0,6λ₂ . Jeżeli i , to λ₁ - λ₂ = 0,04λ₂ .

Dla λ₁ - λ₂ = 0,012λ₂ .

Jeżeli układ UW jest określony inaczej to różnica λ₁ - λ₂ może być inna.

Dla v >> u długości skoków w obydwu detektorach są w przybliżeniu równe

.