3.3. Siła grawitacji działająca na punkt materialny znajdujący się wewnątrz materialnej kuli

Weźmy jednorodną materialną kulę, o środku w punkcie S i promieniu d, spoczywającą w układzie OXYZ i znaj­dującą się w dużej odległości od innych cząstek materii. Obliczmy siłę działającą na punkt materialny P znajdujący się wewnątrz tej kuli w odległości r od jej środka.

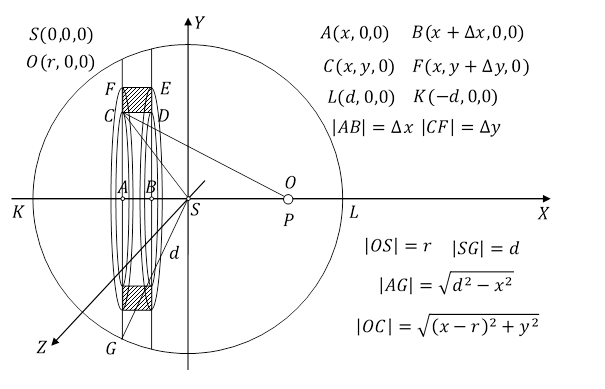
Rys. 3.3.1.

Pęd przekazywany przez grawitony do punktu materialnego określa ten sam wzór, jak w przypadku punktu leżącego na zewnątrz kuli. W obliczeniach musimy uwzględnić, że r < d.

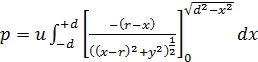
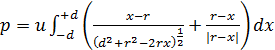
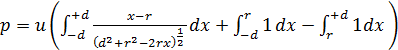
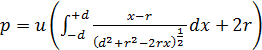
Do całki stosujemy podstawienie jak w 3.2. i otrzymujemy.

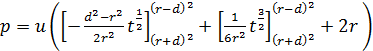
r < d
 

Siła działająca na punkt materialny jest równa

.

Możemy ją przedstawić w innej postaci

.
 

m_kr oznacza masę kuli o środku S i promieniu r.

Dla obserwatora O' mamy

.

Siła działająca na P jest taka, jak gdyby ten punkt materialny znajdował się na powierzchni kuli o środku S i promieniu r'. Na punkt materialny nie działa siła pochodząca z kulistej powłoki o środku S i promieniach r' i d'.

Weźmy materialną wydrążoną kulę ograniczoną dwiema koncentrycznymi sferami o środku S i promieniach i (). Wewnątrz umieśćmy punkt materialny P tak, że .

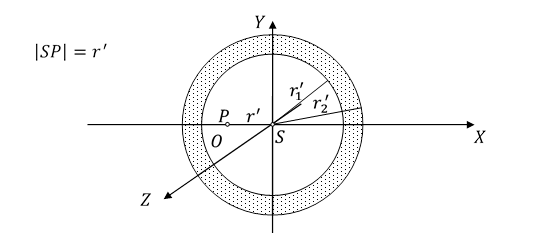
Rys. 3.3.2.

Na cząstkę P nie będzie działała żadna siła, wynikająca z obecności wydrążonej kuli, ponieważ kula o środku S i promieniu r' nie zawiera materii.