4.5. Oddziaływanie materii z cząstkami przestrzeni

Zakładam, że w zwykłych warunkach cząstki materii i przestrzeni są wymieszane ze sobą. Cząstki przestrzeni tworzą gaz, w którym zanurzone są cząstki materii. Cząstki przestrzeni i cząstki materii oddziałują ze sobą tylko za pośrednictwem grawitonów, ale cząstki przestrzeni (tak jak i cząstki materii) mogą oddziaływać ze sobą bez pośrednictwa grawitonów. Wzajemne oddziaływanie cząstek przestrzeni powoduje powstanie pewnego ciśnienia w przestrzeni.

Z cząstką przestrzeni oddziałują grawitony emitowane i absorbowane przez cząstki materii oraz cząstki przestrzeni całego Wszechświata, znajdujące się w odległości d > d_w od tej cząstki. Jeżeli cząstka przestrzeni znajduje się w centralnej części Wszechświata, to suma pędów grawitonów z nią oddziałujących jest wektorem zerowym i z tego powodu nie działają na nią żadne siły. Na cząstki przestrzeni znajdujące się dalej od centrum Wszechświata działają siły RW pochodzące od materii i pozostałej przestrzeni, które starają się oddalić od siebie cząstki przestrzeni.

Jeżeli element objętości przestrzeni ΔV znajduje się w odległości r od ciała materialnego o masie M, to ich wzajemne oddziaływanie grawitacyjne może zmienić w tym elemencie ciśnienie i gęstość cząstek przestrzeni.

Zakładam, że stosunek ciśnienia q wytworzonego przez cząstki przestrzeni do gęstości tych cząstek jest stały dla każdego lokalnego obserwatora O. Przyjmuję, że

gdzie jest stałym, bezwymiarowym współczynnikiem i c jest prędkością światła.

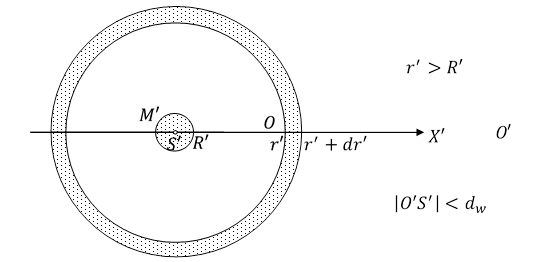
Rys. 4.5.1.

Weźmy materialną kulę o masie M', o środku w punkcie S' i promieniu R', znajdującą się daleko od innych ciał materialnych oraz obserwatora O' daleko od S' i ciał materialnych. W odległości r od punktu S znajduje się element objętości , blisko którego znajduje się obserwator O. Jeżeli dla obserwatora O ciśnienie cząstek przestrzeni w elemencie jest równe q, to dla obserwatora O' ciśnienie w tym elemencie jest

gdzie

q' = qα²

Gęstość cząstek przestrzeni w elemencie dla obserwatora O jest , natomiast dla obserwatora O' jest równa

Dla obserwatora O' mamy

Dla obserwatora O' masa cząstek przestrzeni, znajdujących się w kulistej warstwie o środku S', promieniach r' i r' + dr', jest określona wzorem

gdzie jest gęstością przestrzeni w tej warstwie i

objętością warstwy.

Na warstwę kulistą działa siła

Rzeczywista siła jest większa, ponieważ należałoby uwzględnić oddziaływanie grawitacyjne cząstek przestrzeni znajdujących się wewnątrz kuli o promieniu r'.

Zmiana ciśnienia w warstwie kulistej przy przejściu od r' do r' + dr' jest

Ponieważ

więc

Rozwiązujemy równanie różniczkowe o zmiennych rozdzielonych

dla

W pobliżu obserwatora O' ciśnienie cząstek przestrzeni jest

Gęstość przestrzeni jest równa

Gęstość przestrzeni w otoczeniu obserwatora O' jest równa

Jeżeli przyjąć

Ciśnienie

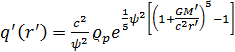
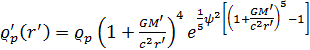
Jeżeli jest małe wówczas mamy następujące wzory.

Gdy odległość r' maleje wówczas ciśnienie q' jak również gęstość rosną.

Jeżeli promień R' materialnej kuli zmniejsza się, to ciśnienie i gęstość cząstek przestrzeni na powierzchni tej kuli odpowiednio zwiększają się.

W skali całego Wszechświata przestrzeń, ze względu na panujące w niej ciśnienie i siły RW działające na cząstki przestrzeni, może się tylko rozszerzać, przy czym szybkość rozszerzania wzrasta wraz z upływem czasu.

W pobliżu materialnych obiektów znajduje się obszar, w którym gęstość cząstek przestrzeni jest większa niż jej wartość średnia. Słońce jest otoczone dość dużym obszarem podwyższonej gęstości cząstek przestrzeni, co powoduje niewielkie zwiększenie siły „przyciągania” działającej na planety; kula przestrzeni o zwiększonej gęstości oddziałuje grawitacyjnie podobnie jak materialna kula. Z tego powodu należy nieco zmodyfikować wzór na przyciąganie dwóch ciał, w prawie powszechnej grawitacji Newtona. Gęstość cząstek przestrzeni w tym obszarze maleje ze wzrostem odległości od Słońca, co dodatkowo komplikuje obliczanie siły działającej na planetę.

Duże obiekty materialne, takie jak galaktyki, są otoczone obszarem cząstek przestrzeni, w którym średnia gęstość cząstek przestrzeni może być znacznie większa w stosunku do średniej gęstości cząstek materii. Centralna część galaktyki o dużej gęstości materii „przyciąga” cząstki przestrzeni, co powoduje wzrost średniej łącznej gęstości materii i przestrzeni. To zwiększanie gęstości powoduje zwiększenie siły „przyciągania” i napływ nowych cząstek przestrzeni aż do wystąpienia równowagi między siłami grawitacji i ciśnieniem wewnętrznym przestrzeni. Galaktyka jest zanurzona w kuli przestrzeni, o dużej gęstości, znacznie większej niż sama galaktyka. Ta kula przestrzeni oddziałuje na ciała materialne znajdujące się wewnątrz niej. Wobec tego na gwiazdę znajdującą się w galaktyce działa siła pochodząca od materii, malejąca ze wzrostem odległości od środka i dodatkowa siła pochodząca od kuli przestrzeni. Wypadkowa tych sił jest większa, niż siła wynikająca z oddziaływania tylko samej materii znajdującej się w galaktyce. Gwiazdy znajdujące się blisko centrum galaktyki poruszają się po orbitach zgodnych z prawem powszechnej grawitacji, natomiast gwiazdy znajdujące się na obrzeżach galaktyki mogą poruszać się znacznie szybciej, niż wynika to z tego prawa.

Jeżeli

i jest minimalną gęstością przestrzeni, to

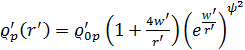
Jeżeli jest małe, to

W dużym przybliżeniu

Na powierzchni kuli o promieniu R' > w' gęstość przestrzeni jest równa

Zakładam, że wewnątrz tej kuli gęstość jest taka sama jak na jej powierzchni. Masa przestrzeni zawarta w tej kuli jest równa

Masa przestrzeni zawarta w warstwie kulistej, o promieniach R' i r' > R', jest równa

Masa przestrzeni w kuli o promieniu r' jest równa

Na punkt materialny o masie m', znajdujący się w odległości r' od środka kuli, działa siła „przyciągania” wywierana przez nadwyżkę masy przestrzeni zawartej w tej kuli ponad wartość minimalną

dla

r' > R' .

Na ten punkt materialny działa również siła „przyciągania”, pochodząca od masy kuli, określona wzorem

Stosunek tych sił jest równy

Stosunek nie zależy od masy kuli i jest wprost proporcjonalny do średniej gęstości materii. Dla małych r' siła ma niewielkie znaczenie, dla dużych r' siła może być znacznie większa od F'. Gdyby w przestrzeni istniała tylko jedna materialna kula, to siła byłaby praktycznie stała w całym Wszechświecie. W rzeczywistości obok jednego materialnego ciała istnieją inne, co powoduje, że gęstość przestrzeni w pewnej odległości od kuli staje się minimalna i nadwyżka masy przestrzeni ponad minimalną jest równa zero. Dla odległości masa jest stała.

Dla odległości siła zmienia się zgodnie z prawem powszechnej grawitacji. Można przyjąć, że jest równe średniej odległości między ciałami. Dla gwiazd w naszej galaktyce ta odległość jest stosunkowo duża, dla galaktyk niewielka.

Weźmy kulę o masie

M' = 10⁹ mas Słońca = 2⋅10³⁹ kg

i promieniu

R' = 10⁴ lat świetlnych = 9⋅10¹⁹ m .

W odległości

r' = 5⋅10⁴ lat świetlnych = 4,5⋅10²⁰ m

od środka kuli stosunek

Przypuśćmy, że

Wówczas

Całkowita siła działająca na punkt materialny znajdujący się w odległości r' jest równa . Na podstawie ruchu gwiazdy znajdującej się w odległości r' od kuli możemy dojść do wniosku, że masa kuli jest prawie 6 razy większa niż w rzeczywistości.

	2⋅10⁴	3⋅10⁴	4⋅10⁴	5⋅10⁴	6⋅10⁴	7⋅10⁴
	1,7⋅F'	2,6⋅F'	4,0⋅F'	5,6⋅F'	8,7⋅F'	10,1⋅F'

Dla większych odległości od środka kuli oddziaływanie grawitacyjne innych ciał może zmienić gęstość przestrzeni i siła może się zmieniać w inny sposób, niż dla mniejszych odległości. W centrum galaktyki ruchy gwiazd są określone prawem powszechnej grawitacji, ponieważ wpływ przestrzeni na nie jest niewielki. Natomiast w większych odległościach od środka ruch gwiazdy jest bardzo skomplikowany, ponieważ oprócz rozkładu materii w galaktyce należy uwzględnić rozkład gęstości przestrzeni, który zależy nie tylko od samej galaktyki, ale również od innych galaktyk.

Dla Układu Słonecznego wpływ przestrzeni jest niewielki.

Masa Słońca

M' = 2⋅10³⁰ kg ,

promień

R' = 6,96⋅10⁸ m.

Dla Ziemi

r' = 1,49⋅10¹¹ m,

Dla Neptuna