2.4. Odległość punktów w polu grawitacyjnym

Dla ustalonego obserwatora współczynnik α zmienia się w zależności od miejsca w przestrzeni układu współrzędnych. Odległość dwóch dalekich punktów, dla obserwatora O', zależy od ich położenia w przestrzeni i jest na ogół różna od odległości mierzonej w prostokątnym układzie współrzędnych.

Rys. 2.4.1.

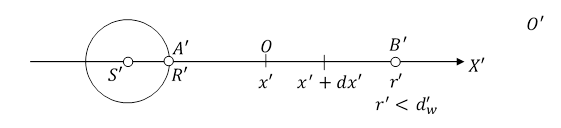
Weźmy kulę o środku w punkcie S', promieniu R' i masie M' w układzie współrzędnych S'X'Y'Z' powstałym przez przesunięcie układu związanego z obserwatorem O', który znajduje się daleko od kuli i innych ciał materialnych. Na osi S'X' są odłożone takie same jednostki długości jak na osiach układu obserwatora O'. Dla obserwatora O' odległość punktów A' i B', w układzie współrzędnych S'X'Y'Z', jest równa

|A'B'| = r' - R'.
 

|S'B'| = r'

Dla obserwatora O' element długości obliczony przez tego obserwatora, przy pomocy własnej jednostki długości, dla miejsca gdzie znajduje się obserwator O, jest określony równaniem

.

Odległość punktów S' i B', obliczona przez obserwatora O', jest równa

.

Odległość punktów A' i B' jest równa

gdzie

i

.
 

Dla odległości punktów S' i A'

.

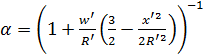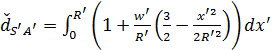
Odległość punktów S' i B', 0bliczona przez obserwatora O' jest równa

dla

r' > R'.

Dla każdego R' i r' > R' odległość . Odległość punktu materialnego od środka kuli zależy od masy kuli i jej promienia. Jeżeli promień kuli zmniejsza się, bez zmiany masy, to odległość ustalonego punktu od środka kuli rośnie. Największa odległość jest wtedy, gdy materia znajduje się w kuli o promieniu w'. Wtedy odległość jest równa

.
 

Również w tym przypadku dla r' > w' odległość .

Weźmy dwie materialne kule o masach i , środkach i , promieniach i , współczynnikach i , dla których odległość środków jest równa r' oraz stosunki i są bliskie zera. Odległość tych kul jest określona wzorem

.

Jeżeli stosunek jest bliski zera, to drugą kulę możemy traktować jak punkt materialny i odległość środków tych kul jest równa

Dla Układu Słonecznego stosunek dla Merkurego, Wenus i Ziemi jest mniejszy od 3,004⋅10^-6, dlatego te planety możemy traktować jak punkty materialne w stosunku do Słońca. Odległość planety od Słońca obliczona przez obserwatora O' jest równa, z dobrym przybliżeniem, odległości w układzie współrzędnych.