2.2. Zmiana tempa upływu czasu i prędkości światła w polu grawitacyjnym
Weźmy materialną kulę o środku w punkcie S i promieniu d oraz punkt materialny P, w odległości r < dw od punktu S. Blisko punktu materialnego znajduje się obserwator O. Daleko od kuli, punktu materialnego i innych ciał znajduje się obserwator O' pozostający w spoczynku względem O. Obserwator O1 może być w dowolnym, ustalonym miejscu przestrzeni. Masy punktu materialnego są równe ![]() ,
, ![]() i
i ![]() odpowiednio dla O, O' i O1. Masa kuli jest bardzo duża w stosunku do masy punktu materialnego i jest równa
odpowiednio dla O, O' i O1. Masa kuli jest bardzo duża w stosunku do masy punktu materialnego i jest równa ![]() dla obserwatora O'.
dla obserwatora O'.
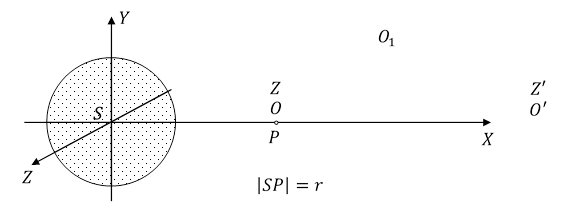
Rys. 2.2.1.
Prostokątny układ współrzędnych SXYZ nie jest układem inercjalnym. Obserwatorzy O i O' mierzą czas własnymi zegarami Z i Z'. Zegary Z i Z' początkowo znajdowały się obok siebie, były identycznie wykonane i tak samo odmierzały jednostki czasu. Każdy obserwator używający swojego zegara otrzyma taką samą wartość liczbową prędkości światła, jeżeli pomiar wykonuje w swoim bliskim otoczeniu.
Dla O masa punktu materialnego jest
![]() .
.
Masa punktu materialnego dla O' jest równa
![]()
i
![]() .
.
Wówczas
![]() ,
,
Δt'α = Δt.
Δt' = Δtα-1.
Jeżeli dla obserwatora O jego własny zegar Z odmierzy Δt jednostek czasu między dwoma zjawiskami, to dla obserwatora O', według jego zegara Z', upłynie
![]()
jednostek czasu między tymi samymi zdarzeniami. Zegar obserwatora O według obserwatora O' tyka wolniej niż jego własny.
W OTW zależność między tempem upływu czasu, dla obserwatorów O i O', w statycznym polu grawitacyjnym wytworzonym przez kulę o masie ![]() i promieniu d, określa wzór
i promieniu d, określa wzór
![]() ,
,
sprawdzony doświadczalnie.
W tej teorii ta zależność jest określona wzorem
![]() .
.
Obserwator O znajduje się w odległości r od środka kuli, natomiast O' jest daleko od kuli i innych ciał materialnych.
Współczynnik
![]() ,
,
natomiast
![]() .
.
Jeżeli
![]()
jest bliskie zera, to w przybliżeniu mamy równość
![]()
i
![]() .
.
Porównując ostatni wzór z odpowiednim wzorem z OTW otrzymujemy
![]() .
.
Dla ![]() , takie efekty jak, ugięcie światła w polu grawitacyjnym, przesunięcie peryhelium planety czy zmiana energii fotonu w polu grawitacyjnym są zgodne z wynikami obserwacji astronomicznych i doświadczeniem.
, takie efekty jak, ugięcie światła w polu grawitacyjnym, przesunięcie peryhelium planety czy zmiana energii fotonu w polu grawitacyjnym są zgodne z wynikami obserwacji astronomicznych i doświadczeniem.
![]()
![]()
Jeżeli za jednostkę długości przyjąć
![]()
i
r = nw,
to
![]()
![]() .
.
Wartości tych współczynników dla niektórych wartości n są przedstawione w następującej tabeli.
| n | ||||
| 100000 | 0,999990 | 0,999990 | 0 | 0% |
| 10000 | 0,999900 | 0,999900 | 0 | 0% |
| 1000 | 0,999001 | 0,998999 | 0,000002 | 0,0002% |
| 100 | 0,990099 | 0,989949 | 0,00015 | 0,015% |
| 10 | 0,909091 | 0,894427 | 0,0147 | 1,61% |
| 5 | 0,833333 | 0,774597 | 0,0587 | 7,05% |
| 4 | 0,800000 | 0,707107 | 0,0929 | 11,61% |
| 3 | 0,750000 | 0,577350 | 0,1727 | 23,02% |
| 2 | 0,666667 | 0 | 0,6667 | 100% |
| 1 | 0,500000 | - | - | - |
Dane z tabeli mają sens dla promienia kuli d spełniającego warunek ![]() . Dla r > 0 współczynnik α > 0. Różnice między
. Dla r > 0 współczynnik α > 0. Różnice między ![]() i
i ![]() są niewielkie dla r > 10w. Dla r > 2w według OTW Δt' = ∞, natomiast w tej teorii grawitacji
są niewielkie dla r > 10w. Dla r > 2w według OTW Δt' = ∞, natomiast w tej teorii grawitacji ![]() . Dla r = w,
. Dla r = w, ![]() traci sens, natomiast α = 0,5 i t' = 2Δt. Tempo upływu czasu może się zmniejszyć najwyżej do połowy. Dla promienia Słońca n = 471500 mamy
traci sens, natomiast α = 0,5 i t' = 2Δt. Tempo upływu czasu może się zmniejszyć najwyżej do połowy. Dla promienia Słońca n = 471500 mamy ![]() .
.
Niech foton przebiegnie odległość między dwoma punktami znajdującymi się blisko obserwatora O w czasie Δt i Δt' odpowiednio dla O i O'. Droga przebyta przez foton, dla obserwatora O, jest równa
Δl = cΔt
i odpowiednio
Δl' = c'Δt'
dla O'. Ponieważ z Założenia 9 wynika, że
Δl'Δt' = ΔlΔt
oraz
Δt = αΔt',
więc
Δl'Δt' = ΔlαΔt'.
Δl' = Δlα
Prędkość tego fotonu dla obserwatora O' jest równa
![]() .
.
![]()
c' = cα2
Prędkość światła w punkcie P dla obserwatora O' jest równa
![]() ,
,
gdzie c jest prędkością światła zmierzoną przez obserwatora O.
Wartość c jest również prędkością światła zmierzoną przez obserwatora O', gdy dokonuje on pomiaru blisko siebie. Natomiast dla O' prędkość światła w pobliżu punktu P jest mniejsza niż c.
Dla O' foton zbliżający się do materialnej kuli zmniejsza swoją prędkość. Prędkość światła ma taką samą wartość dla każdego obserwatora tylko lokalnie, gdy obserwator dokonuje jej pomiaru blisko siebie.
Jeżeli materialna cząstka, znajdująca się blisko obserwatora O, przebędzie odległość Δl i Δl', w czasie Δt i Δt' z prędkością v i v' odpowiednio dla O i O' , to jej szybkość
![]()
![]()
v' = vα2.
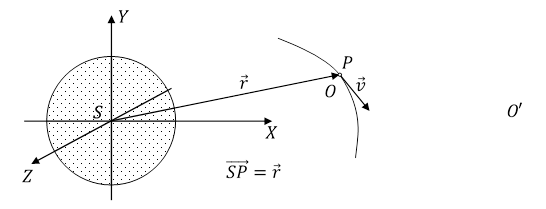
Rys. 2.2.2.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Jeżeli stosunek
![]()
jest mały, to z dobrym przybliżeniem
![]() .
.
![]()
![]()
![]()
![]()
Dla każdego obserwatora można określić współczynnik ![]() wyznaczony dla miejsca gdzie znajduje się obserwator. Dla O, O' i O1 mamy odpowiednio
wyznaczony dla miejsca gdzie znajduje się obserwator. Dla O, O' i O1 mamy odpowiednio ![]() , α' i α1. Dla obserwatora O' znajdującego się daleko od kuli α' = 1.
, α' i α1. Dla obserwatora O' znajdującego się daleko od kuli α' = 1.
Dla obserwatorów O i O' masy punktu materialnego są odpowiednio m i m' = mα (obserwator O znajduje się blisko punktu materialnego).
Dla obserwatora O1 znajdującego się w dowolnym ustalonym miejscu masa tego punktu materialnego jest
![]() .
.
Jeżeli O1 jest blisko O, to
α1 = α
i
m1 = m .
Jeżeli O1 jest blisko O', to
α1 = α' = 1
i
m1 = mα = m' .
m' = mα ![]()
![]()
Analogicznie dla O1 odstęp czasu
![]() .
.
Odstęp czasu Δt jest mierzony bezpośrednio przez obserwatora O.
Δt' = Δtα-1 ![]() Δt1 = Δt'α1
Δt1 = Δt'α1
Jeżeli odcinek znajdujący się blisko O ma długość Δl, to
Δl' = Δlα ![]()
![]() .
.
Jeżeli dla obserwatora O' odległość między odległymi punktami jest l', to dla O1 odległość między tymi punktami jest
![]()
i dla O
![]() .
.
Dla przyspieszenia mamy zależność
![]() .
.
![]()
![]()
![]()
Siła
![]() .
.
![]()
![]()
![]()
Pęd
![]() .
.
![]()
![]()
![]()
Zmiana pędu
![]() .
.
![]()
![]()
![]()
Praca
![]()
![]()
![]()
![]()
Energia
![]() .
.
![]()
![]()
![]()
Stała grawitacji G i stała Plancka h mają taką samą wartość dla każdego obserwatora i w każdym miejscu.
Wartości wielkości fizycznych mogą być mierzone przez obserwatora O lub O' przy pomocy odpowiedniego układu jednostek.
| Pomiar wykonany przez obserwatora O, w układzie jednostek tego obserwatora, w miejscu gdzie znajduje się obserwator O | Odpowiedna wartość tego pomiaru, obliczona przez obserwatora O', dla miejsca gdzie znajduje się obserwator O |
| Δt | Δt' = α-1Δt |
| Δl | Δl' = αΔl |
| c = const. | c' = αΔl |
| m = const. | m' = mα |
| E = mc2 | |
| E = hv | |
W powyższej tabeli wartości Δt, m, p, E, F, Δt', m', p', E', F' mają inne znaczenie niż Δt', m', p', E', F', Δt, m, p, E, F w następnej tabeli.
W pierwszej kolumnie dla obydwu tabel znajdują się wartości zmierzone odpowiednio przez obserwatorów O i O'. W drugiej, w obydwu tabelach, odpowiedna wartość tego pomiaru, obliczona przez obserwatora O', dla miejsca gdzie znajduje się obserwator O.
W pierwszej tabeli obserwator O' oblicza odpowiednie wartości przy pomocy układu jednostek obserwatora O, natomiast w drugiej tabeli przy pomocy własnego układu jednostek.
| Pomiar wykonany przez obserwatora O', w układzie jednostek tego obserwatora, w miejscu gdzie znajduje się obserwator O' | Odpowiedna wartość tego pomiaru, obliczona przez obserwatora O', dla miejsca gdzie znajduje się obserwator O |
| Δt' | Δt = αΔt' |
| Δl' | Δl = α-1Δl' |
| c' = const. | |
| m' = const. | |
| E' = hv' | |
Dla różnych obserwatorów O układy jednostek są różne, dlatego w dalszym ciągu będę na ogół używał jednostek obserwatora O'.